Two touching blocks 1 and 2 are placed on an inclined plane forming an angle 60∘ with the horizontal. The masses are m1 and m2 and the coefficient of friction between the inclined plane and the two blocks are 1.5μ and 10μ, respectively. The force of reaction between the blocks during the motion is (g = acceleration due to gravity)
(m2−m1)μg
(m2+m1)μg
12m1m2m1+m2μg
14m1m2m1+m2μg
The correct Answer is:D
According to the question, there are two blocks of masses m1 and m2 which are kept in contact on inclined plane of inclination 60∘ as shown in the figure,
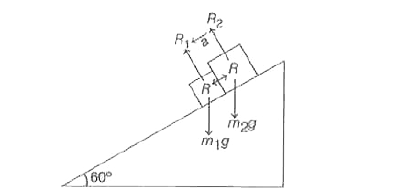
Ceofficient of friction between the surface of plane and syrface of first block, μ1=1.5μ
Coefficient of friction between the surface of place and surface of second block, μ2=1μ
Now, free body diagram for the first block,
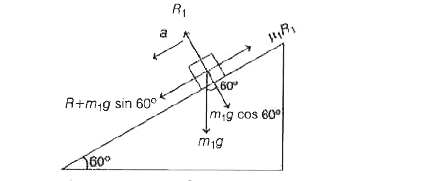
If a be the common acceleration, then
m1gsin60∘−μ1.R1+R=m1a
m1g√32−1.5μm1gcos60∘+R=m1a
m1g√32−1.5μm1g2+R=m1a ...(i)
Similarly, for second body,
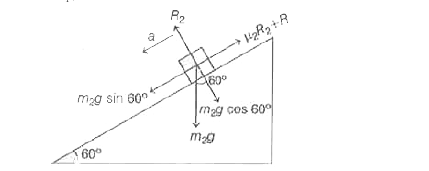
m2gsin60∘−μ2R2−R=m2a
m2g√32−μm2gcos60∘−R=m2a
m2g√32−μm2g2−R=m2a ...(ii)
From Eqs. (i) and (ii), we get
m1g√32−1.5μm1g2+Rm2g√32−μm2g2−R=m1am2a
⇒√32m1m2g−0.75μm1m2g+m2R
=√32m1m2g−0.5μm1m2g−m1R
⇒(m1+m2)R=0.25μm1m2g
⇒R=μm1m2g4(m1+m2)
Hence, the force of reaction between the blocks doing the motion is, R=14m1m2(m1+m2)μg.
Topper's Solved these Questions
Similar Questions
The coefficient of friction between the block and the inclined plane is μ.
View SolutionTwo blocks are in contect moving on an inclined plane of inclination α with the horizontal. The masses of the blocks are equal to m1 and m2 and the coefficients of friction between the inclined plane and the blocks are equal to μ1 and μ2(μ1>μ2) respectively. Find (a) common acceleration of the blocks and (b) the contact force between the blocks.
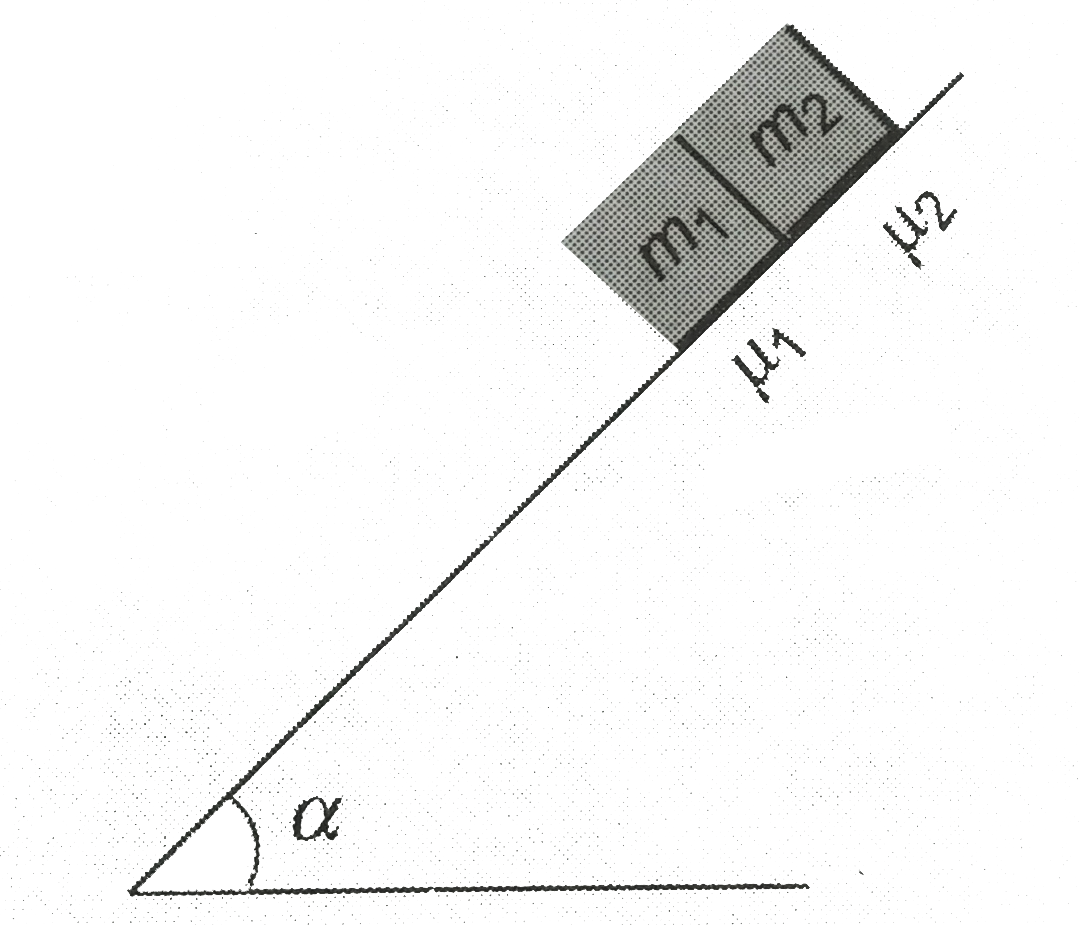
View Solution
Knowledge Check
consider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between block B and inclined plane is μ2 and in between the two, blocks is μ1. The system is released from rest.
(Take g=10m/sec2)
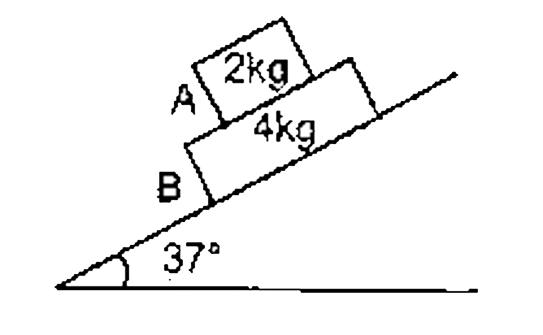
The frictional force acting between the two blocks in the previous question is :A8 NB6 NC4 ND0consider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between block B and inclined plane is μ2 and in between the two, blocks is μ1. The system is released from rest.
(Take g=10m/sec2)
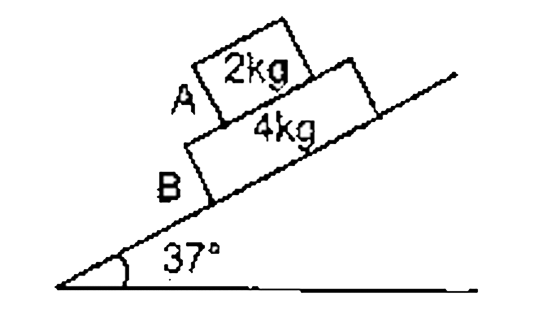
The frictional force acting between the blocks in the previous case :A8 NB6.4 NC6 NDzeroconsider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between block B and inclined plane is μ2 and in between the two, blocks is μ1. The system is released from rest.
(Take g=10m/sec2)
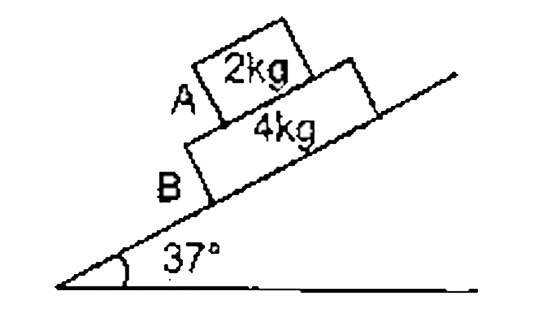
The frictional force acting between the blocks in the previous case will be:A8 NB6.4 NC4 NDzero
A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block is lying on an inclined plane which makes an angle of 60∘ with the horizontal. If coefficient of friction between the block and the plane is 0.25 and g = 10 ms−2, the acceleration of block when it is moves along the plane will be
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View Solution
