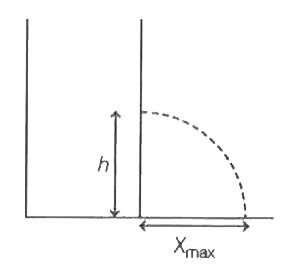
A cylindrical vessel of height 50 cm is filled with water and rests on a table. A small hole is made at the height h from the bottom of the vessel so that the water jet could hit the table surface at a maximum distance xmax from the vessel as shown in the figure. The value of xmax will be (Neglect the viscosity of water.)
15 cm
35 cm
50 cm
40 cm
The correct Answer is:C
Given, height of cylinder, H = 50 cm

The given situation is shown in the figure. Range (maximum distance) is given by
x=2√h(H−h) ....(i)
x will be maximum only when dxdh=0
2.1[h(−I)+(H−h)I]=0
2√h(H−h)−h+(H−h)=0
H−2h=0
∴h=II2
Hence , x will be maximum, when h=H2
∴ From Eqs. (i) we get
xmax=2√H2(H−H2)
=2√H2.H2=H
xmax=50cm
Topper's Solved these Questions
Similar Questions
A wide cylindrical vessel 50cm in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax from the vessel. Find lmax.
View SolutionA wide cylindrical vessel 50cm in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax from the vessel. Find lmax.
View Solution
Knowledge Check
A cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
 Ax is equal if hole is at depth y or H-yBx is maximum for y=H/2CBoth (a ) and (b) are correctDBoth (d) and (d) are wrong
Ax is equal if hole is at depth y or H-yBx is maximum for y=H/2CBoth (a ) and (b) are correctDBoth (d) and (d) are wrongA cylinderical vessel is filled with water up to height H. A hole is bored in the wall at a depth h from the free surface of water. For maximum range h is equal to
AH/4BH/2C3H/4DH
A wide cylindrical vessel 50cm in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax from the vessel. Find lmax.
View SolutionA cylindrical vessel of hieght h and base area S is filled with water. An orifice of area s<<S is made at the bottom of the vessel. Neglection viscosity find how soon the vessel would be emptied.
View SolutionA cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x

View SolutionA cylindrical vessel of height h and base area S is filled with water. An orifice of area s<<S is opened in the bottom of the vessel. Neglecting the viscosity of water, determine how soon all the water will pour out of the vessel.
View SolutionA cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View SolutionA cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View Solution
