A uniform rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is ω . Find increase in length of the rod, if ρ and Y are the density and Young's modulus of the rod respectively,Solution in Telugu
ρω2y4L2
4ρω2L33Y
ρω2L33Y
ρω2L38Y
The correct Answer is:C
Given,
length of uniform rod = L
angular speed = ω
and density of rod =ρ
. When rod is rotated in a horizontal plane, centrifugal force is responsible for increasing the length of rod, which is also equal to stress.
If dl be the change in length of small element dx due to rotation, by application of force dF.

Young's modulus, Y= stressstrain=dF/Adl/x
⇒dl=d.F.xAY
⇒dF=AYdlx ...(i)
Where, dF = centrifugal force due to mass of the element of length, dx
dF=dm.xω2
dF=mL.xdxω2 ....(ii) [∵ Change in mass dm =mLdx]
From Eqs. (l) and (ii), we get
AYdlx=mL.xdxω2
⇒dl=mx2ω2LAY.dx
⇒ Total change in length
l=∫dl=∫L0mx2ω2LAYdx
=mω2L23AY=mAL.ω2L33Y=ρω2L33Y
Topper's Solved these Questions
Similar Questions
Which of the following represents fundamental forces of nature ?
View SolutionMatch the following table.

View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View SolutionA steel rod of length 2l cross-sectional area A and mass M is set rotating in a horizontal plane about an axis passing through its centre and perpendicular to its length with constant angular velocity ω. If Y is the Young's modulus for steel, find the extension in the length of the rod. (Assume the rod is uniform.)
View SolutionA uniform material rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is w. Find increase in length of the rod. It is given that density and Young’s modulus of the rod are r and Y respectively.
View SolutionA uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity o in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is omega . The force applied on the rod by the pivot is
View SolutionA uniform rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is ω . Find increase in length of the rod, if ρ and Y are the density and Young's modulus of the rod respectively,
View SolutionA uniform rod of length l and density ρ is revolving about a vertical axis passing through its one end. If ω is the angular velocity of the rod then the centrifugal force per unit area of the rod is
View SolutionA thin uniform rod of length L and radius r rotates with an angular velocity in a horizontal plane about a vertical axis passing through one of its ends. The density of the material is ρ and Youngs modulus is Y. 1) Find tension in the rod at distance Y from the axis. 2) Find elongation of the rod
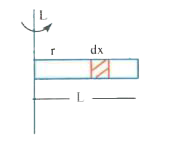
View SolutionA uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity \(omega\) in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity omega about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View Solution
