A wide cylindrical vessel 50cm in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax from the vessel. Find lmax.
The correct Answer is:25
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have a wide cylindrical vessel filled with water, and we need to determine the height h from the bottom of the vessel at which a small hole should be made so that the water jet coming out of it hits the table at the maximum distance Lmax.
Step 2: Apply Bernoulli's Theorem
According to Bernoulli's theorem, the energy per unit volume is conserved. For the water jet, we can equate the potential energy at height H−h to the kinetic energy of the water jet:
12ρv2=ρg(H−h)
Where:
- ρ is the density of water,
- v is the velocity of water coming out of the hole,
- g is the acceleration due to gravity,
- H is the total height of the water (50 cm),
- h is the height from the bottom of the vessel where the hole is made.
Step 3: Solve for Velocity v
From the equation above, we can solve for v:
v=√2g(H−h)
Step 4: Determine the Time of Flight
The water will fall a vertical distance h before hitting the table. The time t taken to fall this distance can be calculated using the equation of motion:
h=12gt2⟹t=√2hg
Step 5: Calculate the Horizontal Range L
The horizontal range L where the water hits the table can be calculated using the formula:
L=v⋅t
Substituting the values of v and t:
L=√2g(H−h)⋅√2hg=2√h(H−h)
Step 6: Maximize the Range L
To find the height h that maximizes L, we differentiate L with respect to h and set the derivative to zero:
dLdh=2(12√h(H−h)(H−h)−12√h(H−h)h)=0
This simplifies to:
H−2h=0⟹h=H2
Step 7: Calculate h and Lmax
Given H=50cm:
h=502=25cm
Now, substituting h=25cm back into the equation for L:
Lmax=2√25(50−25)=2√25⋅25=2⋅25=50cm
Final Answers
- The height h from the bottom of the vessel should be 25 cm.
- The maximum distance Lmax is 50 cm.
---
We have a wide cylindrical vessel filled with water, and we need to determine the height h from the bottom of the vessel at which a small hole should be made so that the water jet coming out of it hits the table at the maximum distance Lmax.
According to Bernoulli's theorem, the energy per unit volume is conserved. For the water jet, we can equate the potential energy at height H−h to the kinetic energy of the water jet:
- ρ is the density of water,
- v is the velocity of water coming out of the hole,
- g is the acceleration due to gravity,
- H is the total height of the water (50 cm),
- h is the height from the bottom of the vessel where the hole is made.
From the equation above, we can solve for v:
The water will fall a vertical distance h before hitting the table. The time t taken to fall this distance can be calculated using the equation of motion:
The horizontal range L where the water hits the table can be calculated using the formula:
To find the height h that maximizes L, we differentiate L with respect to h and set the derivative to zero:
Given H=50cm:
- The height h from the bottom of the vessel should be 25 cm.
- The maximum distance Lmax is 50 cm.
Similar Questions
Water level is maintained ina cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.

View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
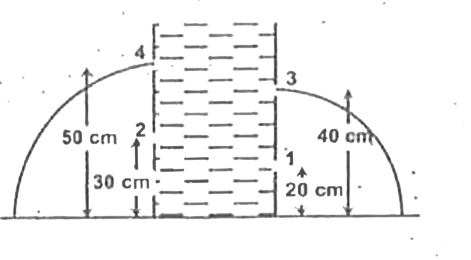
View SolutionFigure shows a cylindrical vessel of height 90 cm filled upto the brim . There are four holes in the vessel as shows in figure . The liquid falling at maximum horizontal distance from the vessel would come from
View SolutionA wide vessel with a small hole in the bottom is filled with water and kerosene. Find the velocity of water flow if the thickness of water layer is h1=30cm and that of kerosene is h2=20cm brgt

View SolutionA small object is placed at the centre of the bottom of a cylindrical vessel of radius 3 cm and height 4 cm filled completely with water. Consider the ray leaving the vessel through a corner. Suppose this ray and the ray along the axis of the vessel are used to trace the image. Find the apparent depth of the image and the ratio of real depth to the apparent depth under the assumptions taken. Refractive index -of water = 1-33.
View SolutionWater drains out of a vessel filled with water upto height h through a hole of area A in t seconds.If the height of the water is 4 h then how much time will be required for the water to drain out ?[Assume A<<A0 (area of tank ) ]
View SolutionA rectangular tank of height 10m filled with water, is placed near the bottom of a plane inclined at an angle 30∘ with horizontal. At height h form bottom a small hole is made (as shown in figure) such that the stream coming out from hole, strikes the inclined plane normally. Calculate h.

View SolutionTo what height h should a cylindrical vessel of diameter d be filled with a liquid so that the total force on the vertical surface of the vessel be equal to the force on the bottom-
View Solution
