The sides of a triangle have the combined equation x2−3y2−2xy+8y−4=0 . The third side, which is variable, always passes through the point (−5,−1) . Find the range of values of the slope of the third line such that the origin is an interior point of the triangle.

A

2<m<5

B

−1<m<15

C

−5<m<−1

D

−7<m<−5

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

x2−2xy−3y2+8y−4=0
⇒(x+y−2)(x−3y+2)=0
& equation of sides are L1,x+y−2=0 & L2:x−3y+2=0
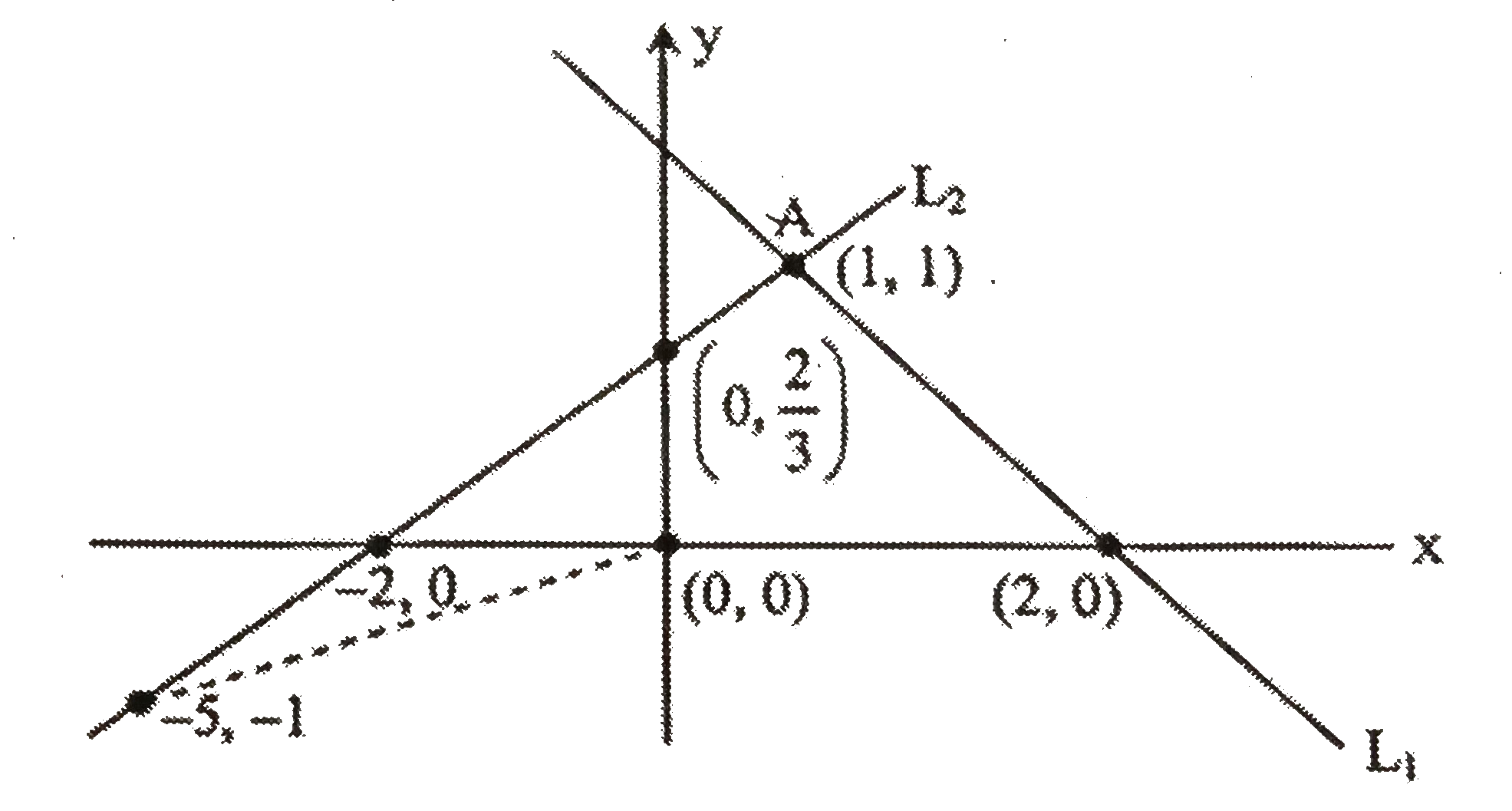
ocr_image
Any line through (−5,−1) having slope m is
L3:y+1=m(x+5)
If L3 is parallel to L1 (i.e, slope m=−1)then none of Δ is possibe & when slope of L3 is m=15 then origin will lie on third side.
∴−1<m<15

Updated on:21/07/2023
|
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The equation of two equal sides of an isosceles triangle are 7x - y + 3 = 0 and x + y - 3 = 0 and its third side is passes through the point (1, - 10). The equation of the third side is

    Ax−3y−7=0 or 3x+y−31=0
    Bx−3y−31=0 or 3x+y−7=0
    Cx−3y−31=0 or 3x+y+7=0
    DNone of these

  • The equation of two equal sides of an isosceles triangle are 7x - y + 3 = 0 and x + y - 3 = 0 and its third side is passes through the point (1, - 10). The equation of the third side is

    Ax−3y=−31
    Bx−3y=31
    Cx+3y=31
    Dx+3y=−31

  • The equation of two equal sides of an isosceles triangle are 7x - y + 3 = 0 and x + y - 3 = 0 and its third side is passes through the point (1, - 10). The equation of the third side is

    Ax - 3y = - 31
    Bx - 3y = 31
    Cx + 3y = 31
    Dx + 3y = - 31