A circle of radius $2$ lies in the first quadrant and touches both the axes. Find the equation of the circle with centre at $(6, 5)$ and touching the above circle externally.

A

$x^{2} + y^{2} - 12 x - 10 y + 52 = 0$

B

$x^{2} + y^{2} - 12 x - 10 y + 12 = 0$

C

$x^{2} + y^{2} - 12 x - 10 y - 52 = 0$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

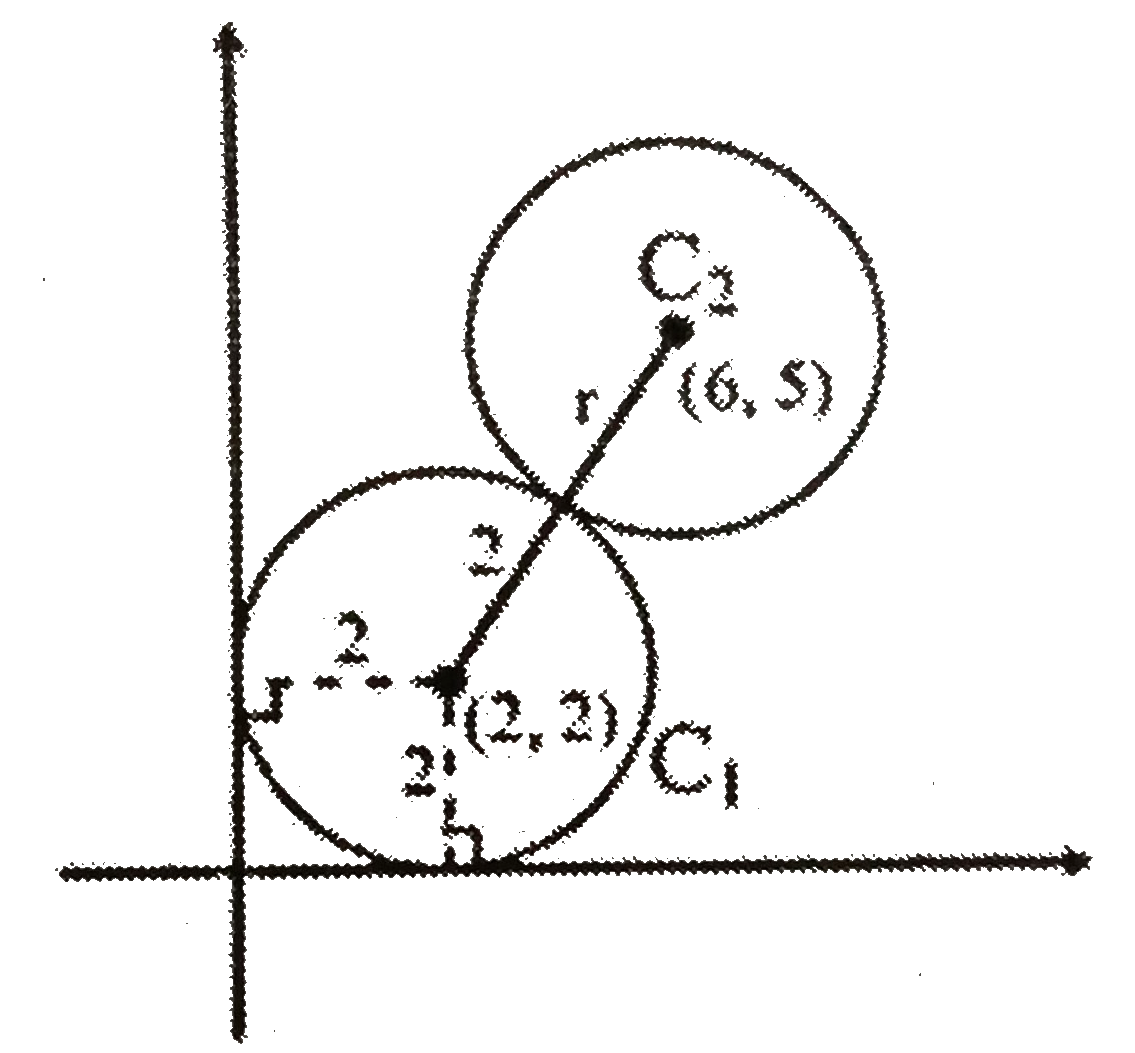
Distance between $C_{1}$ & $C_{2}$
$C_{1} C_{2} = 2 + r$
$\sqrt{{(6 - 2)}^{2} + {(5 - 2)}^{3}} = 2 + r$
$5 = 2 + r$
$\Rightarrow r = 3$
$∴$ Equation of the required circle
${(x - 6)}^{2} + {(y - 5)}^{2} = 3^{2}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
The equation of circle passing through (-1,-2) and touching both the axes is
A $x^{2} + y^{2} - 2 x - 2 y - 1 = 0$
B $x^{2} + y^{2} + 2 x + 2 y + 1 = 0$
C $x^{2} + y^{2} + 10 x + 10 y + 25 = 0$
D $x^{2} + y^{2} - 2 x - 2 y + 1 = 0$
Question 2 - Select One or More
The equation of a circle passing through (3,6) touching both the axes is
A $x^{2} + y^{2} - 6 x - 6 y + 9 = 0$
B $x^{2} + y^{2} + 6 x - 6 y + 9 = 0$
C $x^{2} + y^{2} + 30 x - 30 y + 225 = 0$
D $x^{2} + y^{2} - 30 x - 30 y + 225 = 0$
Question 3 - Select One
The equations of the circles which touch both the axes and the line x = a are
A $x^{2} + y^{2} \pm a x \pm a y + \frac{a^{2}}{4} = 0$
B $x^{2} + y^{2} + a x \pm a y + \frac{a^{2}}{4} = 0$
C $x^{2} + y^{2} - a x \pm a y + \frac{a^{2}}{4} = 0$
Dnone of these

CAREER POINT-MOCK TEST 6-Part (C) (MATHS)

Home
Ask Doubt
Profile