Given that a right angled trapezium has an inscribed circle. Prove that the length of the right angled leg is the Harmonic mean of the lengths of bases

A

Harmonic mean of length of bases

B

Geometric mean of length of bases

C

Arithmetic mean of length of bases

D

None of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

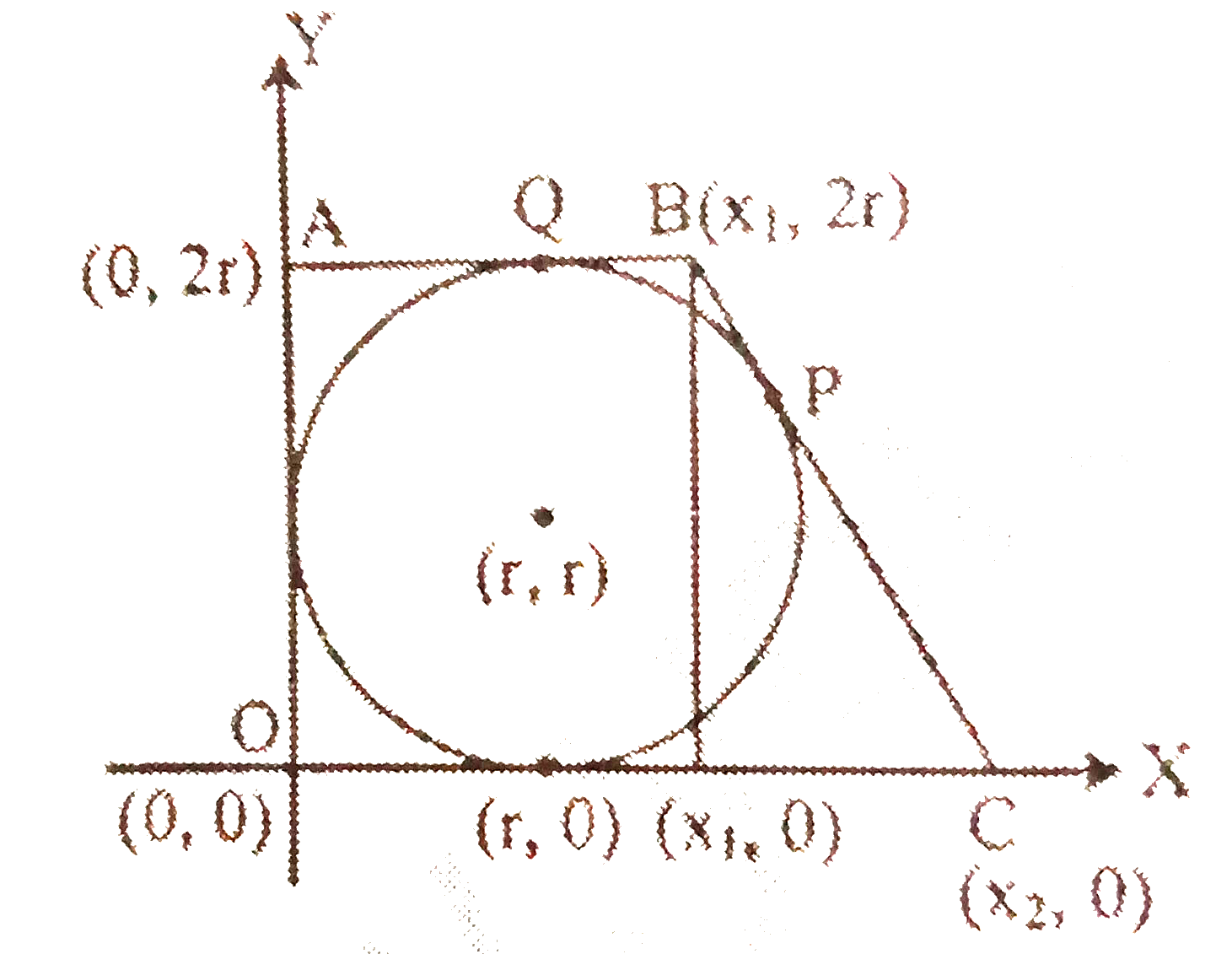
ocr_image
Let length of right angled leg = 2 r = O A
∴ Equation of circle is
( x - r ) 2 + ( y + r ) 2 = r 2 ….. ( i )
∴ Length of tangent
B P = B Q = ( x 1 - r ) 2 + ( 2 r - r ) 2 - r 2
= x 1 - r
Simliarly length of tangent P C = x 2 - r
Now B C = B P + P C
( x 2 - x 1 ) 2 + 4 r 2 = x 1 + x 2 - 2 r
Square
( x 2 - x 1 ) 2 + 4 r 2 = ( x 1 + x 2 ) 2 + 4 r 2 - 4 r ( x 1 + x 2 )
⇒ x 1 x 2 = r ( x 1 + x 2 ) → 1 r = 1 x 2 + 1 x 1
⇒ r = x 1 x 2 x 1 x 2 ⇒ 2 r = 2 x 1 x 2 x 1 + x 2

Updated on:21/07/2023
|
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Base of a right angled triangle is

    A√(Hypotenous)2+(Perpendicular)2
    B√(Hypotenous)2−(Perpendicular)2
    C√(Perpendicular)2−(Hypotenous)2
    DNone of These

  • If the length of sides of right angled triangle are in AP, then their ratio is

    A3:4:5
    B2:3:4
    C1:2:3
    Dnone of these

  • The radius of a circle is 20% more than the height of a right-angled triangle. The base of the triangle is 36 cm. If the area of triangle and circle be equal, what will be the area of circle? (a) 72 cm2 (b) 128 cm2 (c) 144 cm2 (d) 216 cm2 (e) Cannot be determined

    A72 sq cm
    B144 sq cm
    C216 sq cm
    D128 sq cm