A steel wire of mass μ per unit length with a circular cross-section has a radius of 0.1cm. The wire is of length 10m when measured lying horizontal, and hangs from a hook on the wall. A mass fo 25kg is hung from the free end of the wire. Assume the wire to be uniform and laterla strain << logitudinal strain. If density of steel is 7860kgm−3 and Young's modulus is 2×1011N/m2 then the extension in the length fo the wire is
Consider the diagram when a small element of length dx is considered at x from the load (x = 0).
(a) Let T (x) and T (x + dx) are tensions on the two cross-sections a distance dx apart, then -- - T (x+dx) + T(x) = dmg = μdxg (where μ is the mass/length). (∵dm=μdx)
dT=μgdx [∵dT=T(x+dx)−T(x)]
⇒ T(x)=μgx+C (on integrating)
At x=0,T(0)=Mg ⇒ C=Mg
∴ T(x)=μgx+Mg
Let the length dx at x increase by dr, then
Young's modulus Y = StressStrain
T(x)/Adr/dx=Y
⇒ drdx=1YAT(x)
⇒ r=1YA∫L0(μgx+Mg)dx
=1YA[μgx22+Mgx]L0
=1YA[mgL22+MgL]
A=π×(10−3)2m2
Y=200×109Nm−2
m=π×(10−3)2×10×7860kg
∴ r=12×1011×π×10−6 [π×786×10−3×10×102+25×10×10]
=[196.5×10−6+3.98×10−3]≈4×10−3m
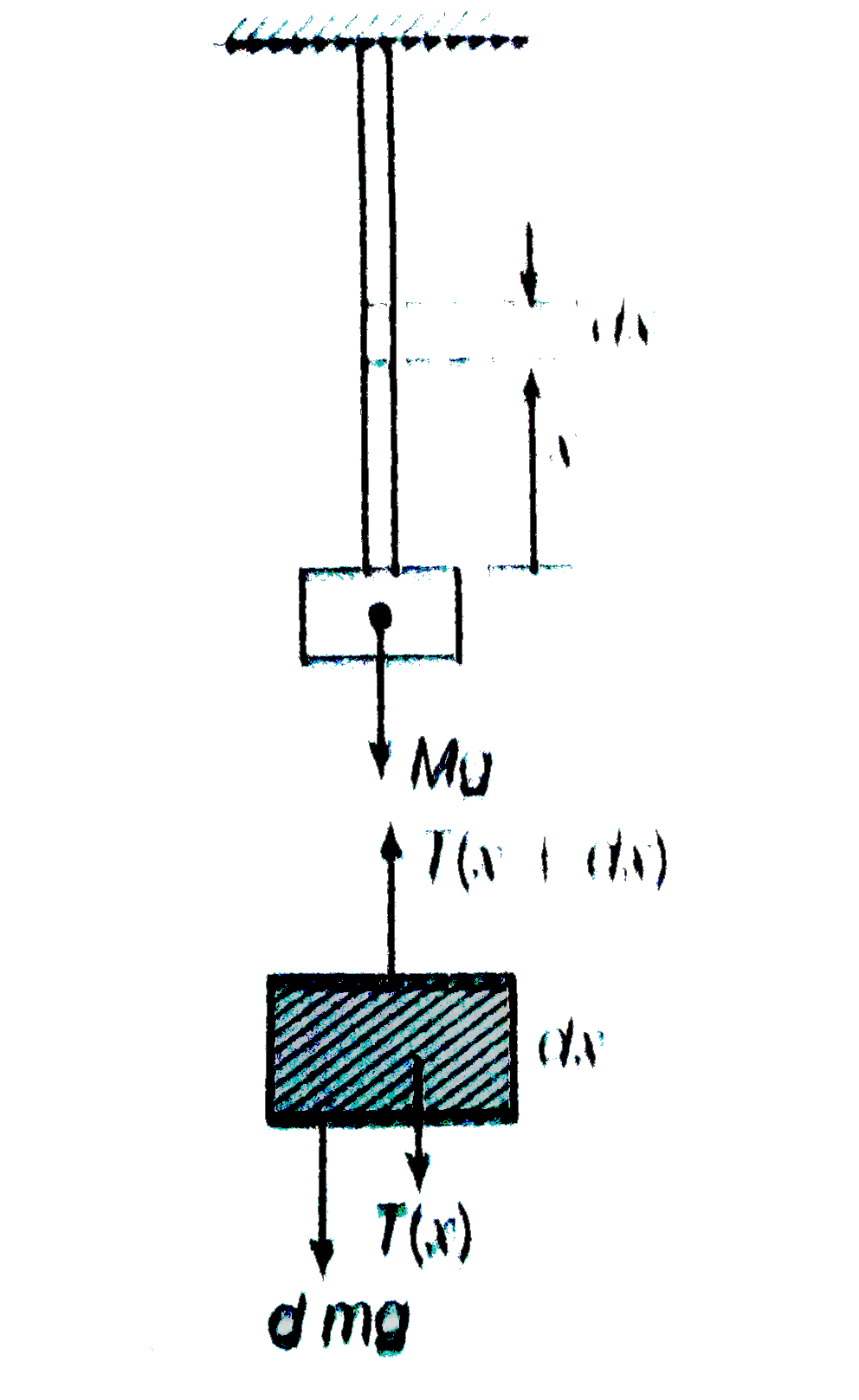
(b) Clearly tension will be maximum at x = L
∴ T=μgL+Mg=(m+M)g [∵m=μL]
The yield force = (Yield strength Y) area =250×106×π×(10−3)2=250×πN
AT yield point T = yield force
⇒ (m+M)g=250×π
m=π×(10−3)2×10×7860<<M
∴ Mg≈250×π
Hence, M=250×π10=25×π≈75kg.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLARCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LONG SHORT ANSWER TYPE QUESTION16videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT EXEMPLARCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Long Answer Type Questions3videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT EXEMPLARCHAPTER - MOTION IN A PLANEEXERCISE - Multiple Choice Questions37videos
MOTION IN A PLANE
Similar Questions
Compute the elongation of the steel wire in the figure. Unloaded length of the steel wire =1.5 m, the diameter of the wire is 0.25 m, Young's modulus of steel is 2×1011 N m−2.
View SolutionA steel wire4.0m in length is stretched through 2.0mm.The cross -sectional area of the wire is 2.0mm2.If young's modulus of steel is 2.0×1011N/m2
(a) the enrgy density of wire,
(b) the elastic potential energy stored in the wire.View Solution
Knowledge Check
- Question 1 - Select One
A mild steel wire of length 2L and cross-sectional area A is stretched, well with in the elastic limit, horizontally between two pillars as shown in figure. A mass m is suspended from the mid-point of the wire strain in the wire is
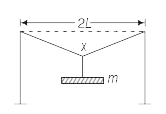 Ax22L2BxLCx2LDx22L
Ax22L2BxLCx2LDx22L - Question 2 - Select One
A steel wire 4.0 m in length is stretched through 2.0 mm. The cross-sectional area of the wire is 2.0mm2. If young's modulus of steel is 2.0×1011Nm−2, then find the energy density of wire.
A2.5×104Jm−3B0.5×104Jm−3C1.6×104Jm−3D3.6×104Jm−3 - Question 3 - Select One
A steel wire of length 2.5 m and area of cross section 1.25mm2, when it is stretched by a force of 40 N and Y for steel is 2×1011N/m2. The extension produced in a steel wire is
A0.4 mmB0.4 cmC4 mmD4 cm
In figure the upper wire is made of steel and the lower of copper. The wires have equal cross section. Find the ratio of the longitudinals strains developed in the two wires.
 View Solution
View SolutionA mild steel wire of length 1.0m and cross sectional area 5.0×10−2cm2 is stretched, within its elastic limit horizontally between two pillars. A mass of 100g is suspended form the midpont of the wire. Calculate the depression at the midpoint (Ysteel=200GPa)
View SolutionA steel wire 2m long is suspended from the ceiling. When a mass is hung from its lower end, the increase in length recorded is 1cm. Determine the strain in the wire.
View SolutionA steel wire of diameter 1 mm, and length 2 m is stretched by applying a force of 2.2 kg wt. the strain is
View SolutionA mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
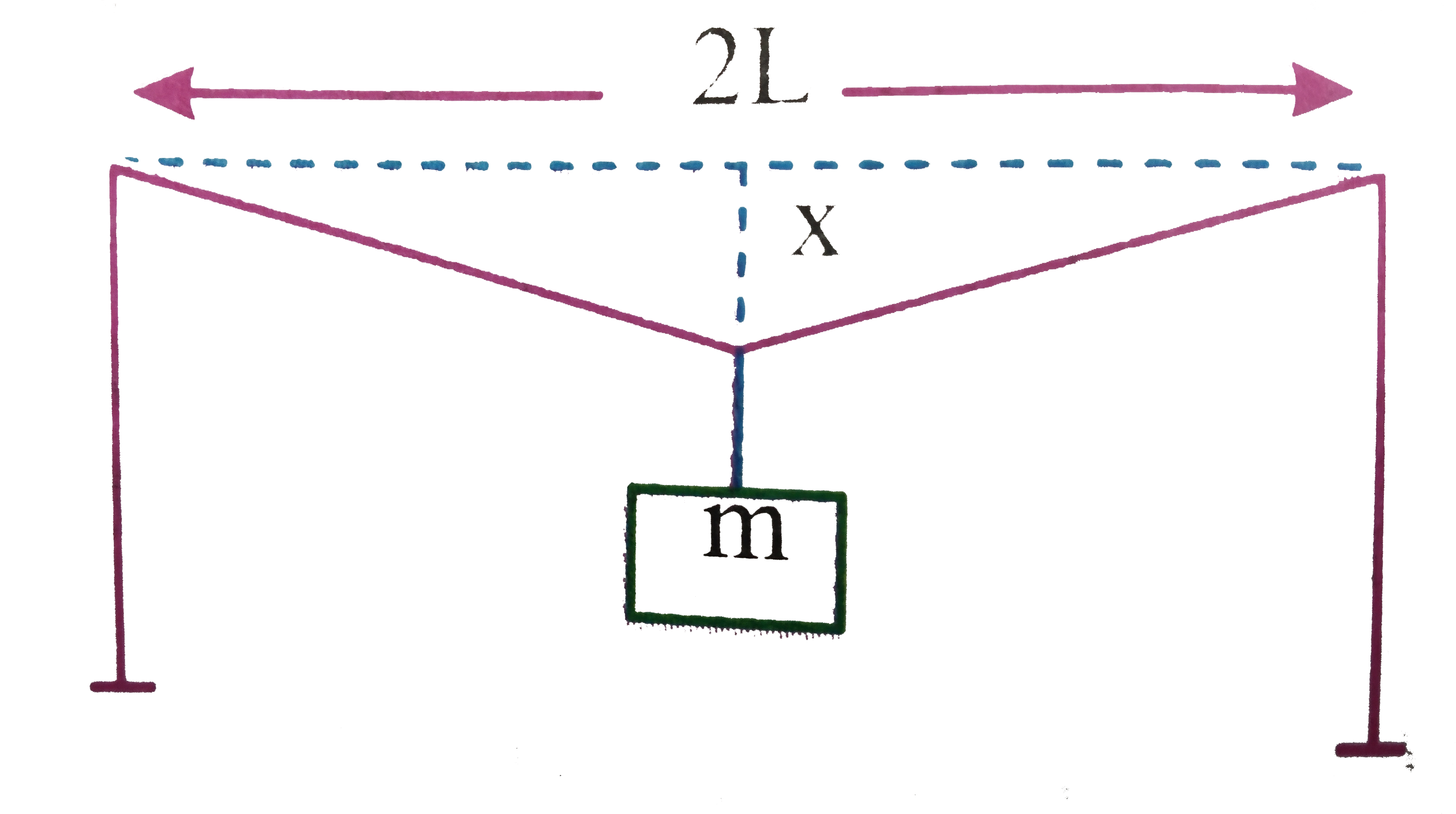 View Solution
View Solution

