An elastic cord of constant K and length L is hung from point A having a massless lock at the other end. A smooth ring of mass M falls from point A , the maximum elongation of cord is

mgK(1+1+2KLMg)
MgK(1−(1−2KLMg)1/2)
MgLK
MgK(1+(1+2KLMg)1/2)
[4]
Let extension in cord is X
Mg(L+x)=12Kx2
⇒Kx2−2Mgx−2MgL=0
x=2Mg±√4M2g2+8KMgL2K
=MgK{1+√2KLMg}
Topper's Solved these Questions
Similar Questions
AB is a vertically suspended elastic cord of negligible mass and length L. Its force constant is k=4mgL. There is a massless platform attached to the lower end of the cord. A monkey of mass m starts from top end A and slides down the cord with a uniform acceleration of g2 . Just before landing on the platform, the monkey loses grip on the cord. After landing on the platform the monkey stays on it. Calculate the maximum extension in the elastic cord.
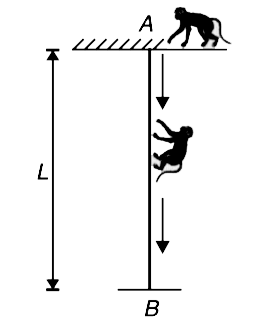
View SolutionThe mass of an uniform ladder of length l increases uniformly from one end A to the other end B,
find the position of the centre of mass from end A.
View Solution
Knowledge Check
A metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
AThe loss in gravitational potential energy of mass M is Mgl.BThe elastic potential energy stored in the wire is MglCThe elastic potential energy stored in the wire is 12MglDHeat produced is loss of mechanical energy of system is 12MglAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
A(a) 4MgkB(b) 2MgkC(c) MgkD(d) Mg2kA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
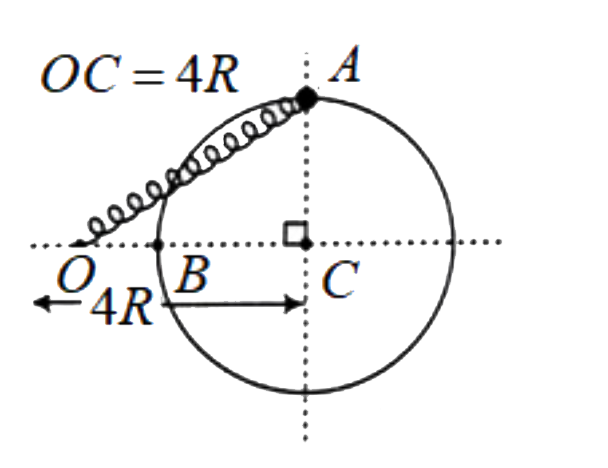 A252kR2B92kR2C8kR2D12KR2
A252kR2B92kR2C8kR2D12KR2
A smooth rubber cord of length l whose coefficient of elasticity is k is suspended by one end from the point O (figure). The other end is fittetd with a catch B. A small sleeve A of mass m starts falling from the point O. Neglecting the masses of the thread and the catch, find the maximum elongation of the cord.
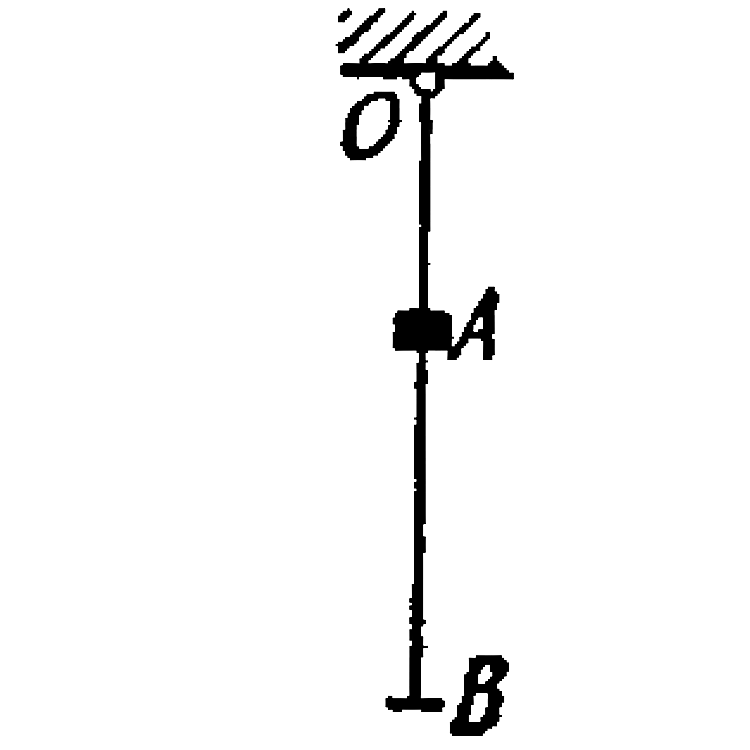
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionAn elastic cord having an upstretched length l, force constant k and mass per unit length m∘ is stretched arouond the drum of radius (2πr>l)
Determine the speed of the cord, due to rotation of te drum, which will allow the cord to loosen its contact with the drum. Express value of v211 (in m2/s2)
( for the given data m0=40g/cm,k=100Nm,π=227,l=400cm,r=70cm)

View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.

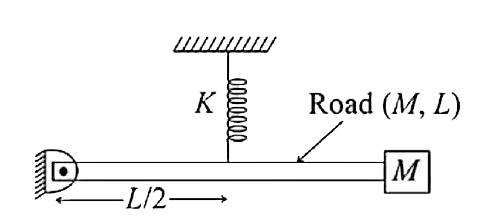
View SolutionA rod of mass 'M' and length'
L' is hinged about one end and a
particle of mass 'M' is
attached to its other end If it is
kept horizontal with the help of
a spring of spring constant 'K'
as shown in fig. find the
extension in spring :-
View Solution
