A circular table with smooth horizontal surface is rotating at an angular speed ω about its axis. A groove is made on the surface along a radius and a small particle is gently placed inside the groove at a distance l from the centre. Find the speed of the particle with respect to the table as its distance from the centre becomes L.
v=ωl
v=ω(l−a)
v=ω(l+a)2
v=ω√l2−a2
a=ω2xorvdvdx=ω2x
∫v0vdv=∫taω2xdx
v=ω√l2−a2
Topper's Solved these Questions
Similar Questions
_S01_013_Q01.png)
A very small groove is made in the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle fro that place.
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View Solution
Knowledge Check
A table with smooth horiztonal surface is truning at an angular speed ω abouyt its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
Av=ω2(L2−a2)13Bv=ω(L2−a2)Cv=ω2√L2−a2Dv=ω√L2−a2A coin placed on a rotating table just slip when it is placed at a distance 4 r from the centre, on doubling the angular velocity of the table , the coin will just slip now the coin is at a distance from centre is
A4 rBr/4CrD2 rA disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
Aμ0αωR3Bμ0αωR36Cμ0αωR38Dμ0αωR33
A rod of length l is rotating with an angular speed ω about its one end which is at a distance a from an infinitely long wire carrying current i.Find the emf induced in the rod at the instant shown in the figure.

View SolutionA rod of length l is rotating with an angular speed ω about one of its ends which is at a distance a from an infinitely long wire carrying current i. Find the emf induecd in the rod at the instanr shown in .
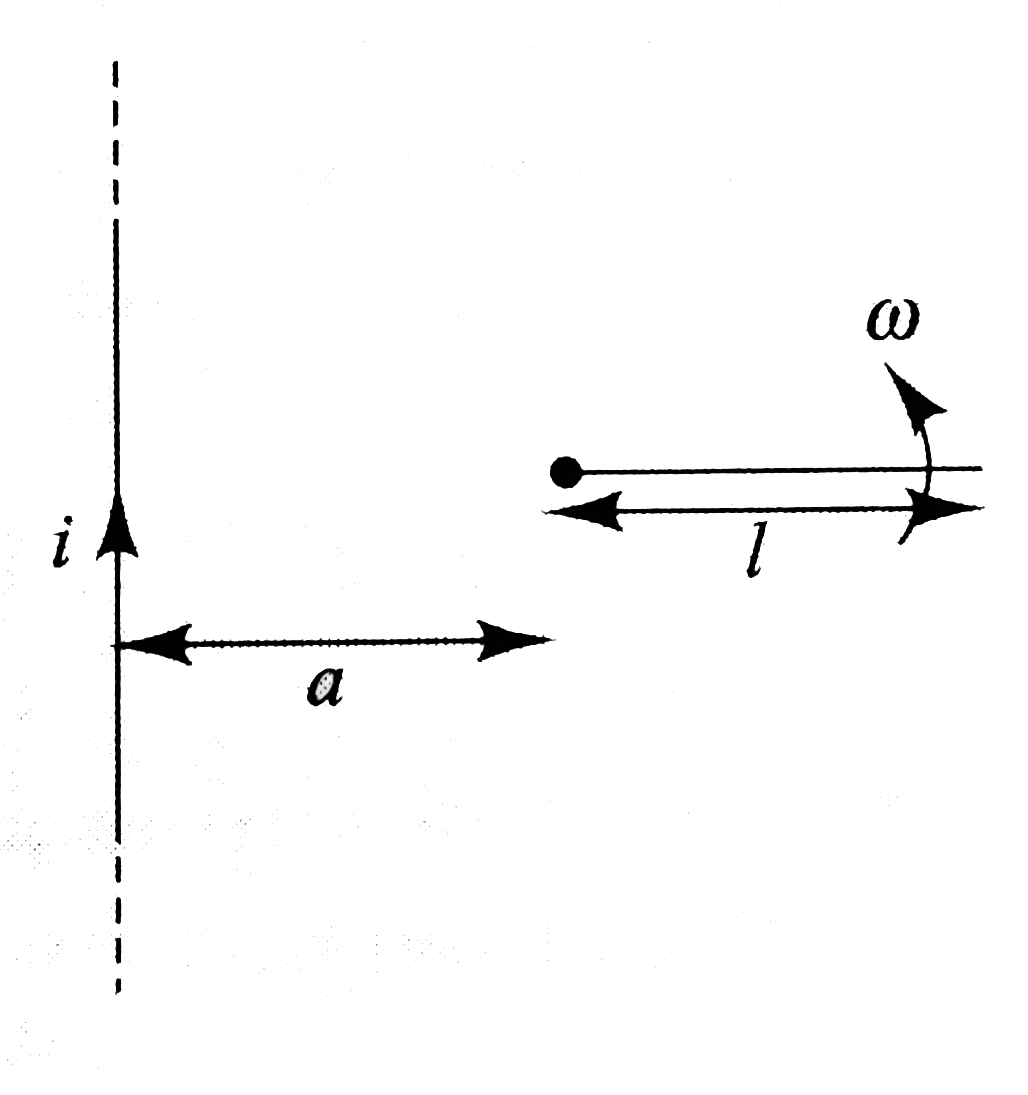
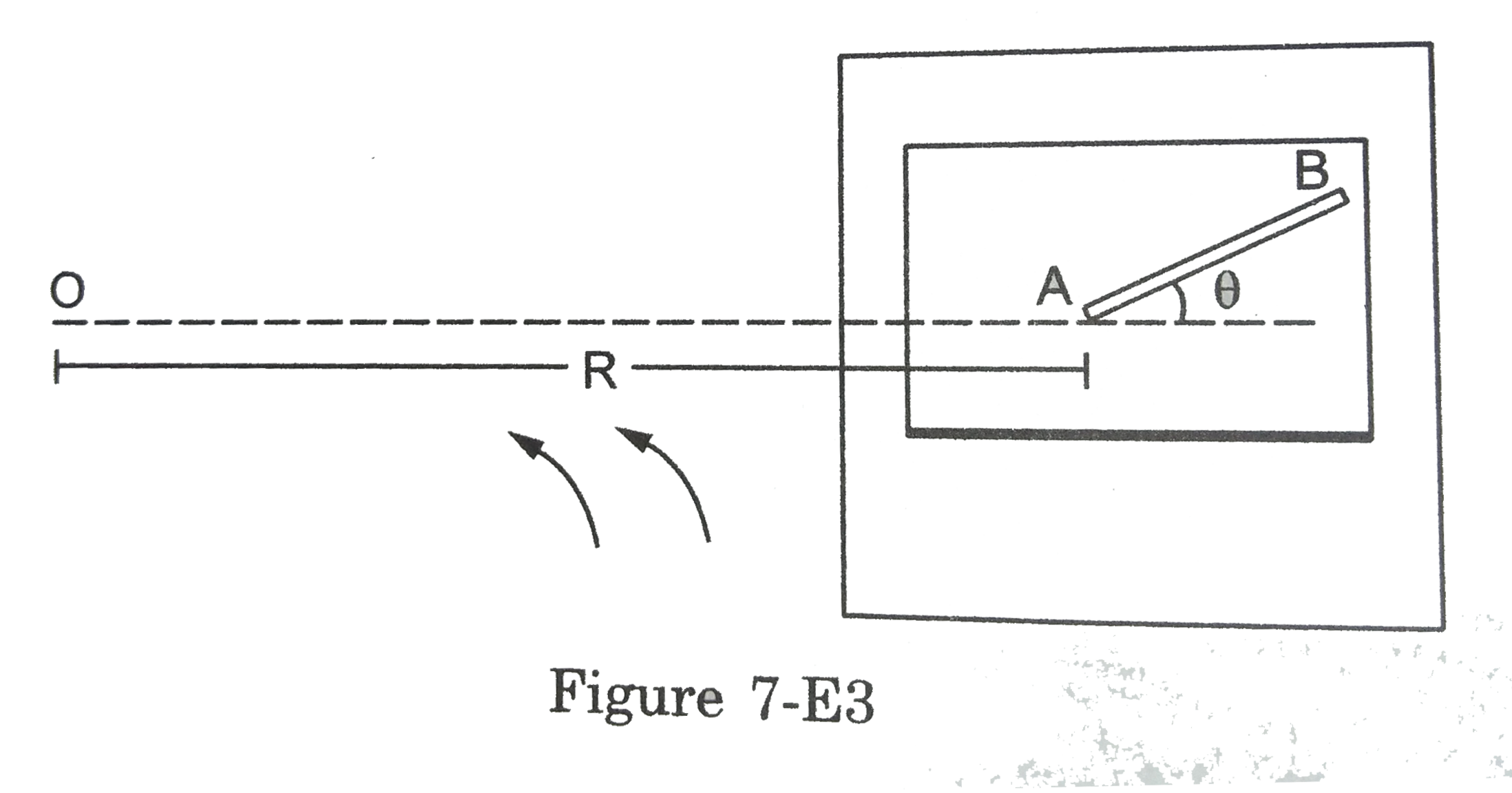
View SolutionA table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular pathof radius R. A smooth groove AB of length L(<<R) is made on the surface of the table. The groove makes an angleθ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move along AB. Find the time taken by tehparticle to reach the point B.
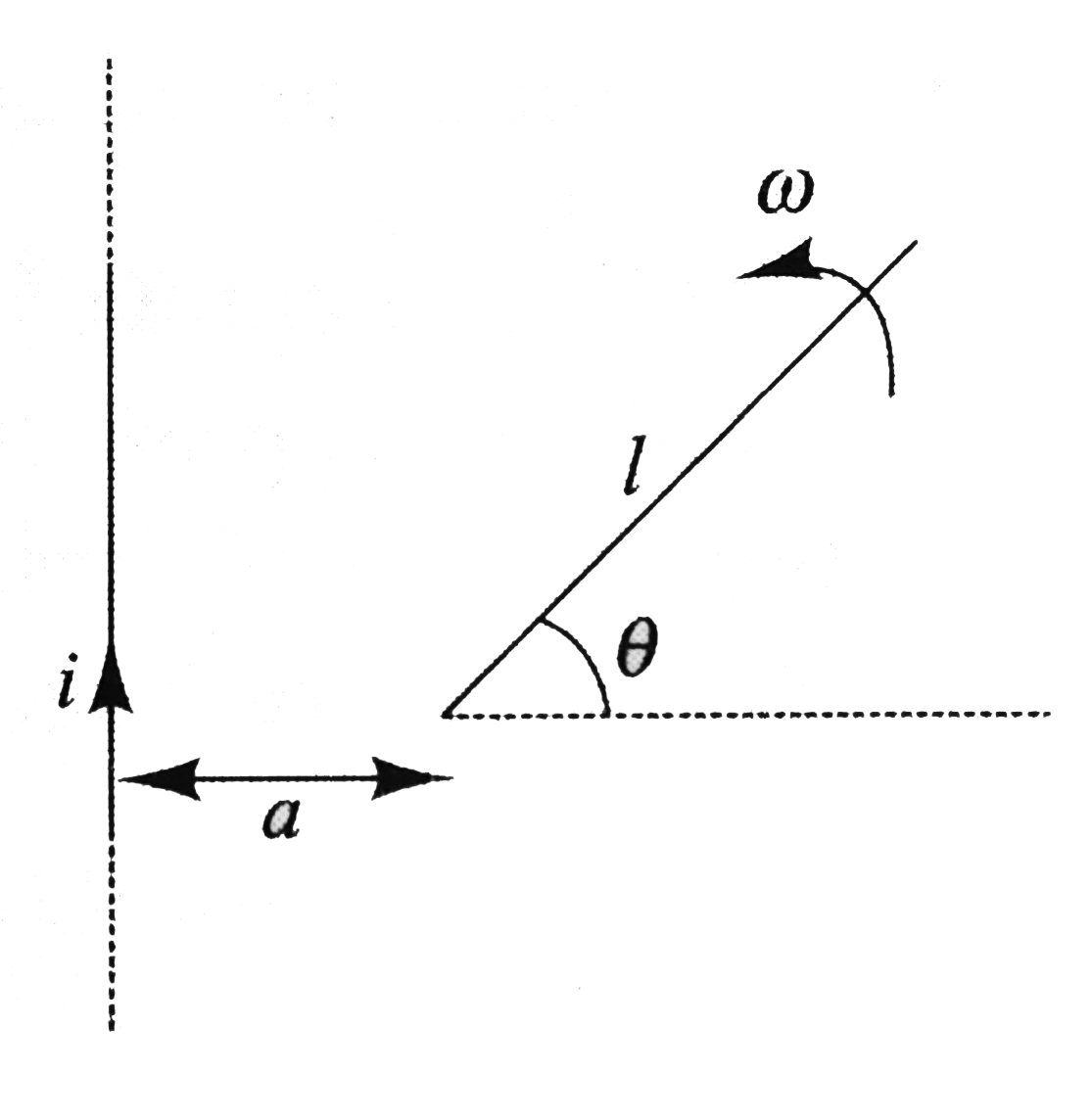
View SolutionA rod of length l is rotating with an angular speed ω about one of its ends which is at a distance a from an infinitely lonf wire carrying current i. Find the emf induced in the rod at the instant shown in .
View SolutionA coin is place at a distance 9 cm from centre on a rotating turn table slip. If the angular velocity of the turn table is tripled, then the distance ofn the coin from the centre will be
View Solution
