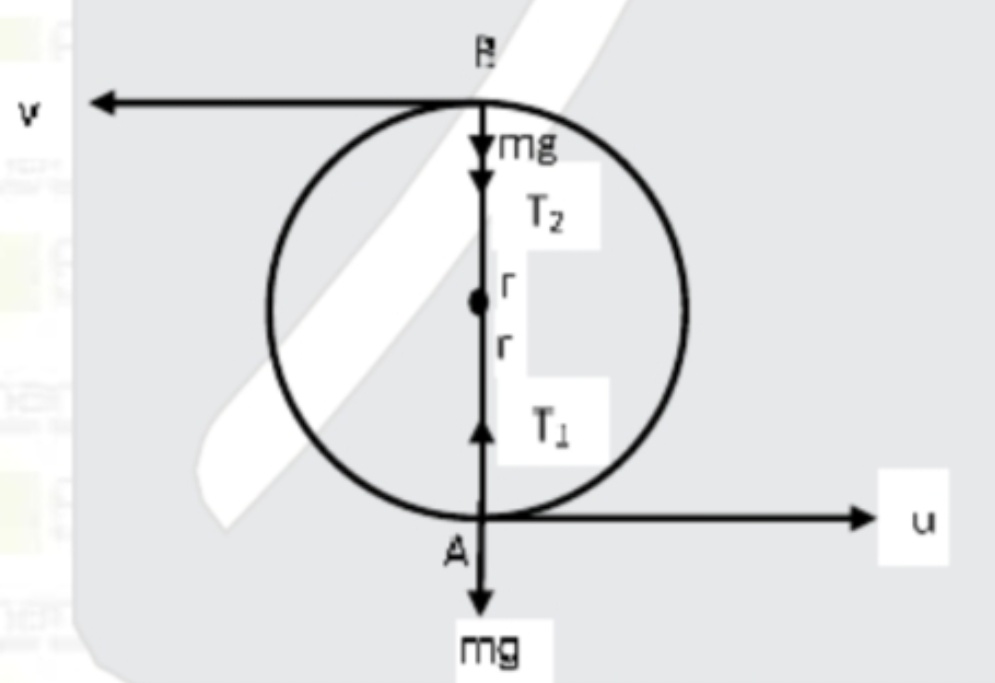
A particle crosses the topmost point C of a vertical circle with critical speed , then the ratio of velocities at points A, B and C is

$3 : 2 : 1$

5 : 3 : 1

$5^{2} : 3^{2} : 1^{2}$

$\sqrt{5} : \sqrt{3} : \sqrt{1}$

Video Solution

Text Solution

Verified by Experts

[4]
$v_{e} = \sqrt{g} R, v_{A} = \sqrt{5} g R, v_{n} = \sqrt{3} g R$
$v_{A} : v_{B} : v_{C} : : \sqrt{5} : \sqrt{3} : 1$

Updated on:21/07/2023

A body attached at one end of a string crosses the topmost point of a vertical circle with the critical speed Its centripetal acceleration , when the string is horizontal will be
Ag
B3g
C5g
D6g
A body crosses the topmost point of a vertical circle with a critical speed. Its centripetal acceleration, when the string is horizontal will be
A $6 g$
B $3 g$
C $2 g$
D $g$
A mass attached to one end of a string crosses top - most point on a vertical circle with critical speed. Its centripetal acceleration when string becomes horizontal will be
(where, g=gravitational acceleration)
Aglancing angle
B3g
C4g
D6g