A railway track is banked for aspeed v, by making the height of the outer rail 'h' higher than that of the inner rail.The horizontal separation between the rails is d. The radius of curvature of the track is 'r': then which of the following relationis true?
hd=v2rg
tan{(sin−1)hd}=V2rg
tan−1hd=v2rg
hr=v2dg
[1]
tanθ=hd=v2rg
Topper's Solved these Questions
Similar Questions
A train has to negotitate a curve of radius 2000m. By how much should the outer rail be raised with respect to inner rail for a speed72km/h. The distance between the rails is 1m.
View SolutionA beaker of radius r is filled with water (refractive index 43) up to a height H as shown in the figure on the left. The beaker is kept on a horizontal table rotating with angular speed ω. This makes the water surface curved so that the difference in the height of water level at the centre and the circumference of the beaker is h (h<<H,h<<r) as shown in the figure on the right . Take this surface to be approximately spherical with a radius of curvalture R . Which of the following is/are correct ? (g is acceleration due to gravity)
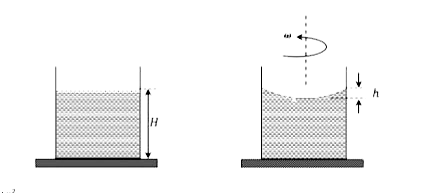
View Solution
Knowledge Check
A railway track is banked for a speed v, by making the height of the outer rail h higher than that of the inner rail. The distance between the rails is d. The radius of the curvature of the track is r
Ahd=v2rgBtan(sin−(h)d)=v2rtCtan−1(hd)=(v2rg)Dhr=v2dgA railway track is banked for a speed v, by making the height of the outer rail h higher than that of the inner rail. If the distance between the rails is l and the radius of the curvature of the track is r, then
Ahl=v2rgBtan{sin−1(hl)}=v2rgCtan−1(hl)=v2rgDhr=v2lgA railway line is banked with an angle of 0.01 radians. The height of the outer rail over inner rail, if the distance between the two rails of 1.5m, will be
A0.025 mB0.035 mC0.015 mD0.045 m
The outer rail of a curved railway track is generally raised over the inner. Why?
View SolutionA car moves along a horizontal circular road of radius r with constant speed v. The coefficient of friction between the wheels and the road is μ. Which of the following statement is not true ?
View SolutionA train has to negotiate a curve of radius 800 m. By how much height should the outer rail be raised with respect to inner rail for a speed of 96kmh−1? The distance between the rails is 1 m
View SolutionA conducting rod with resistance r per unit length is moving inside a vertical magnetic field B with spee v on two smooth horizontal parallel ideal conducting rails. The end of the rails are connected to a resistor R. the separation between the rails is d. The rod maintains a tilted angle θ to the rail. Find the external force F required to keep the rod moving
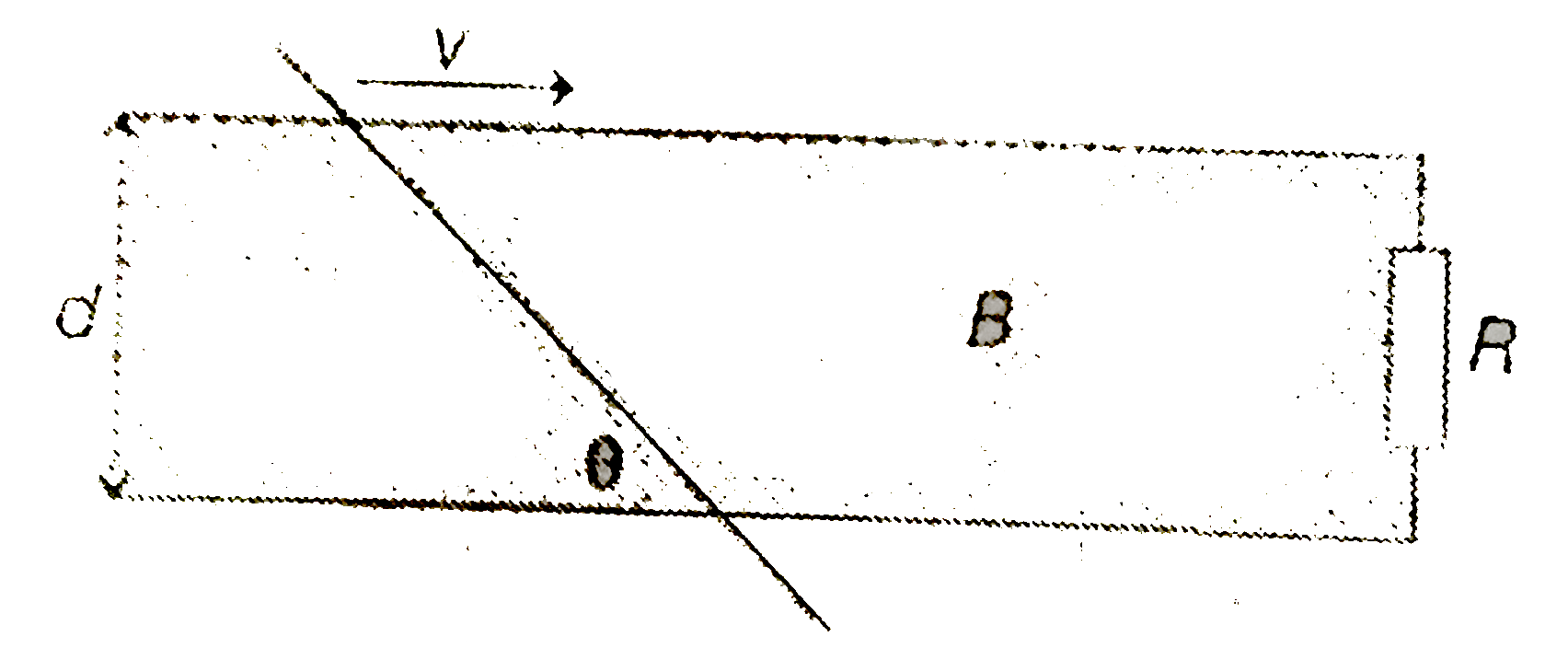
View SolutionTwo parallel rails of a railway track insulated from each other and with the ground are connected to a millivoltmeter. The distance between the rails is one metre. A train is traveling with a velocity of 72kmph along the track. The reading of the millivoltmetre (in mV) is : (Vertical component of the earth's magnetic induction is 2×10−5T)
View Solution
