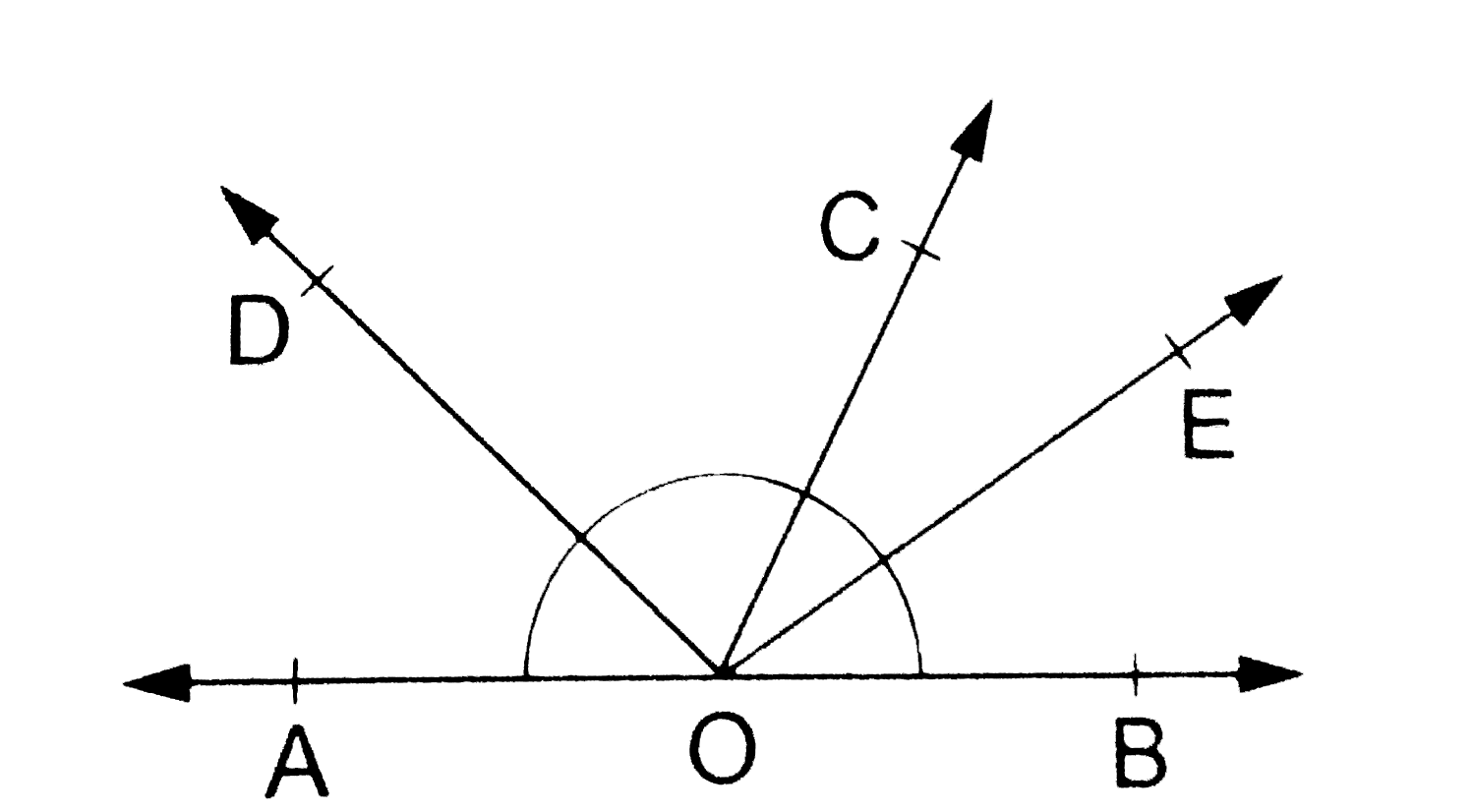
In Fig. 6.10, ray OS stands on a line
POQ. Ray OR and ray OT are angle bisectors of ∠POS
and ∠SOQ
,
respectively. If ∠POS=x
, find ∠ROT
.

Step by step video & image solution for In Fig. 6.10, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of /_P O S and /_S O Q , respectively. If /_P O S=x , find /_R O T . by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
In Figure, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ respectively. If ∠POS=x, find ∠ROT
 View Solution
View SolutionIn the given figure, ray OC stands on a straight line AOB. Ray OD and ray OE are the bisectors of ∠AOC and ∠BOC respectively. Find the measure of ∠DOE.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The number of P-O-P bonds present in P4O6andP4O10 are respectively
A5,5B5,6C6,6D6,5
In Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
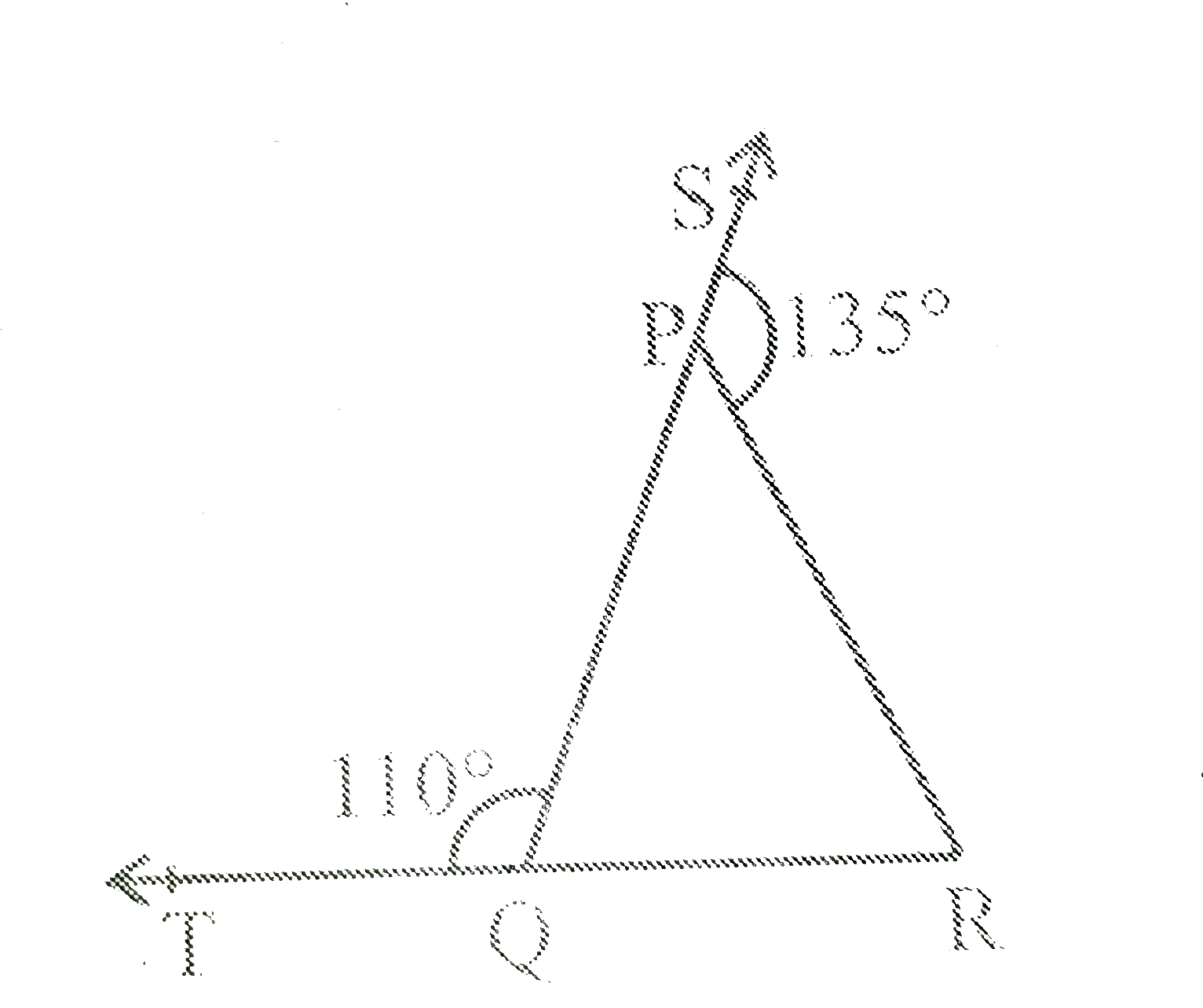 View Solution
View SolutionIn Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS).
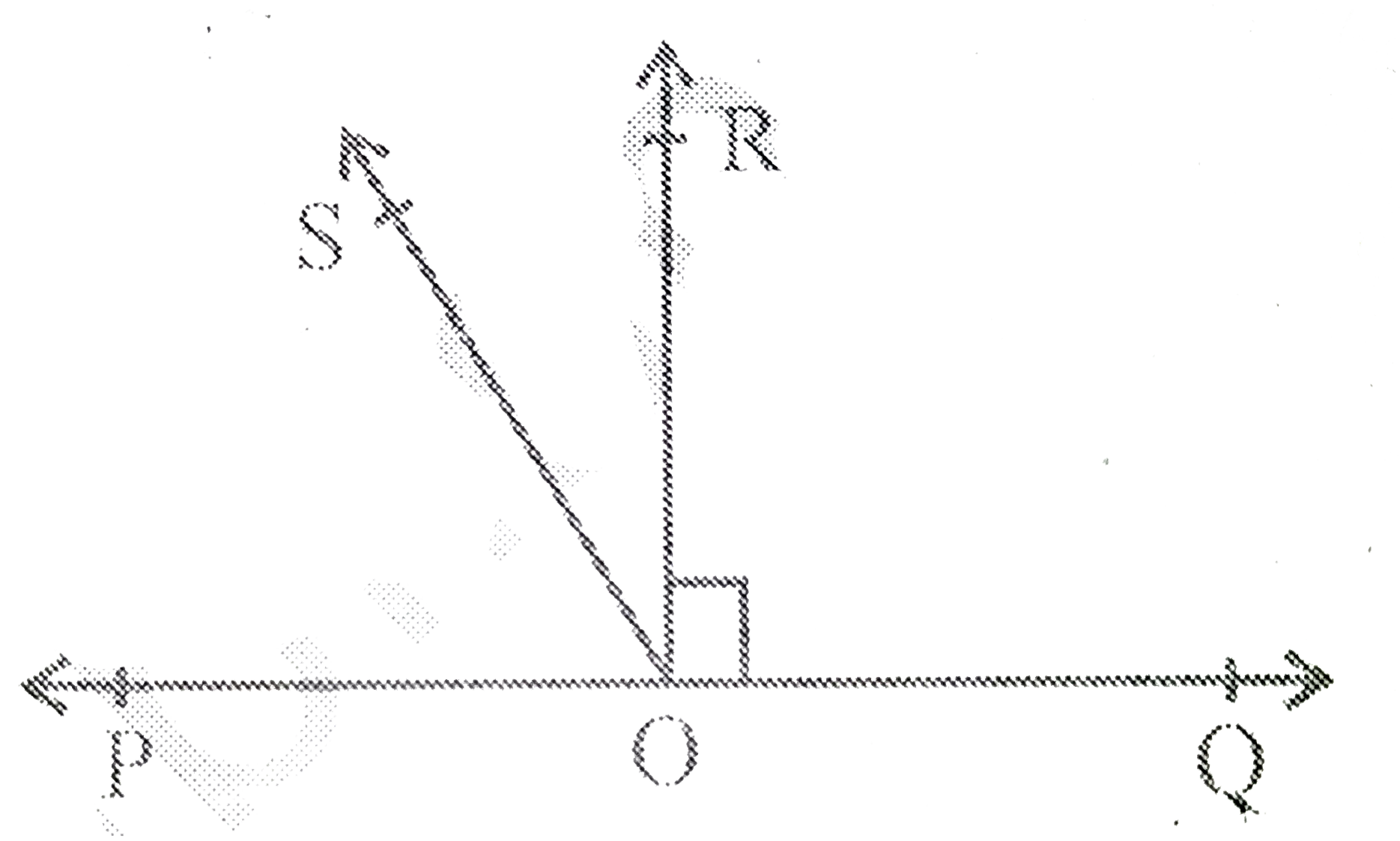 View Solution
View SolutionIn Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q . Line LOM is drawn parallel to PQ . Prove that: PL=QM (ii) LO=OM
View SolutionIn Fig. 4.90, if PSQR , prove that POS~ROQ . (FIGURE)
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.
 View Solution
View SolutionIn ΔPQR, ray PS is the bisector of ∠QPR.
Q−S−R. If QS=4.8cm,SR=3.6cm then find PQ:PR.View SolutionIn fig: 6.14, lines XY and MN intersect at O. If ∠POY=90∘and a:b=2:3, find c.
 View Solution
View Solution

