Of all the line segments drawn from a point P to a line m not containing P, let PD be the shortest. If B and C are points on m such that D is the mid-point of BC , prove that PB=PC.
24114 PB is the shortest
Therefore PD⊥M
∠PDB=∠PDC=900
In △PDB and △PCD
PD=PD....(common)
△PDB=△PDC.................(By ∠900)
BD=DC (given)
Therefore △PDB≅△PDC.........(SAS)
By CPCT
PB=PC
Hence the proved.
Topper's Solved these Questions
Similar Questions
Of all the line segments drawn from a point P to a line m not containing P, let PD be the shortest. If B and C are points on m such that D is the mid-point of BC , prove that PB=PC.
View SolutionOf all the lines segments drawn from a point P to a line m not containing P, let PD be the shortest. If B and C are points on m such that D is the mid-point of BC , prove that PB=PC
View SolutionIn Figure, ABCD and PQRC are rectangles and Q is the mid-point of AC . Prove that DP=PC (ii) PR=12 AC
View SolutionOf all the line segments that can be drawn to a given line, from a point, not lying on it, the perpendicular line segment is the shortest. GIVEN : A straight line l and a point P not lying on l. PM⊥l and N is any point on 1 other than M. TO PROVE : PM<PN
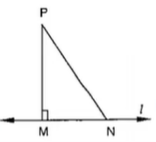 View Solution
View SolutionBM and CN are perpendicular to a line passing through the vertex A of a triangle ABC. If L is the mid-point of BC , prove that LM=LN
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionIn a triangle ABC , let PandQ be points on ABandAC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View Solution

