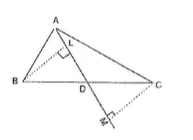
In Figure, AD
is a median and BL,CM
are perpendiculars drawn from B
and C
respectively on AD
and AD
produced. Prove that BL=CM.

Step by step video & image solution for In Figure, A D is a median and B L ,C M are perpendiculars drawn from B and C respectively on A D and A D produced. Prove that B L=C Mdot by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, AD is a median and BL, CM are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BL=CM
View SolutionIn Figure, AD is a median and BL,CM are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BL=CM.

View SolutionIn the adjoining figure, D is the mid-point of BC. If BM and CN are perpendiculars from B and C respectively on AD and AD produced, then prove that BM = CN.

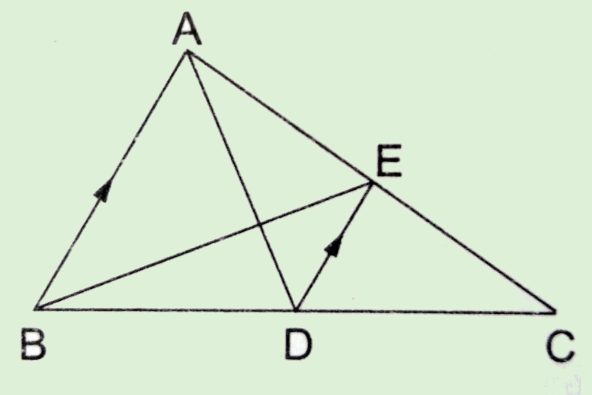
View SolutionIn Figure, AD is the median and DE∣∣AB . Prove that BE is the median.
View SolutionIn a ABC, BM and CN are perpendiculars from B and C respectively on any line passing through A. If L is the mid-point of BC , prove that ML=NL .
View SolutionIn ABC , AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O , prove that: (i) OMAOLC (ii) OAOC=OMOL
View SolutionBD is one of the diagonals of a quadrilateral ABCD. AM and CN are the perpendiculars from A and C , respectively, on BD. Show That ar (qua..ABCD)=12BD.AM+CN
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD

View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View SolutionIn a ABC , If LandM are points ABandAC respectively such that LMparallelBC
Prove that: ar(ABM)=ar(ACL)
View Solution
