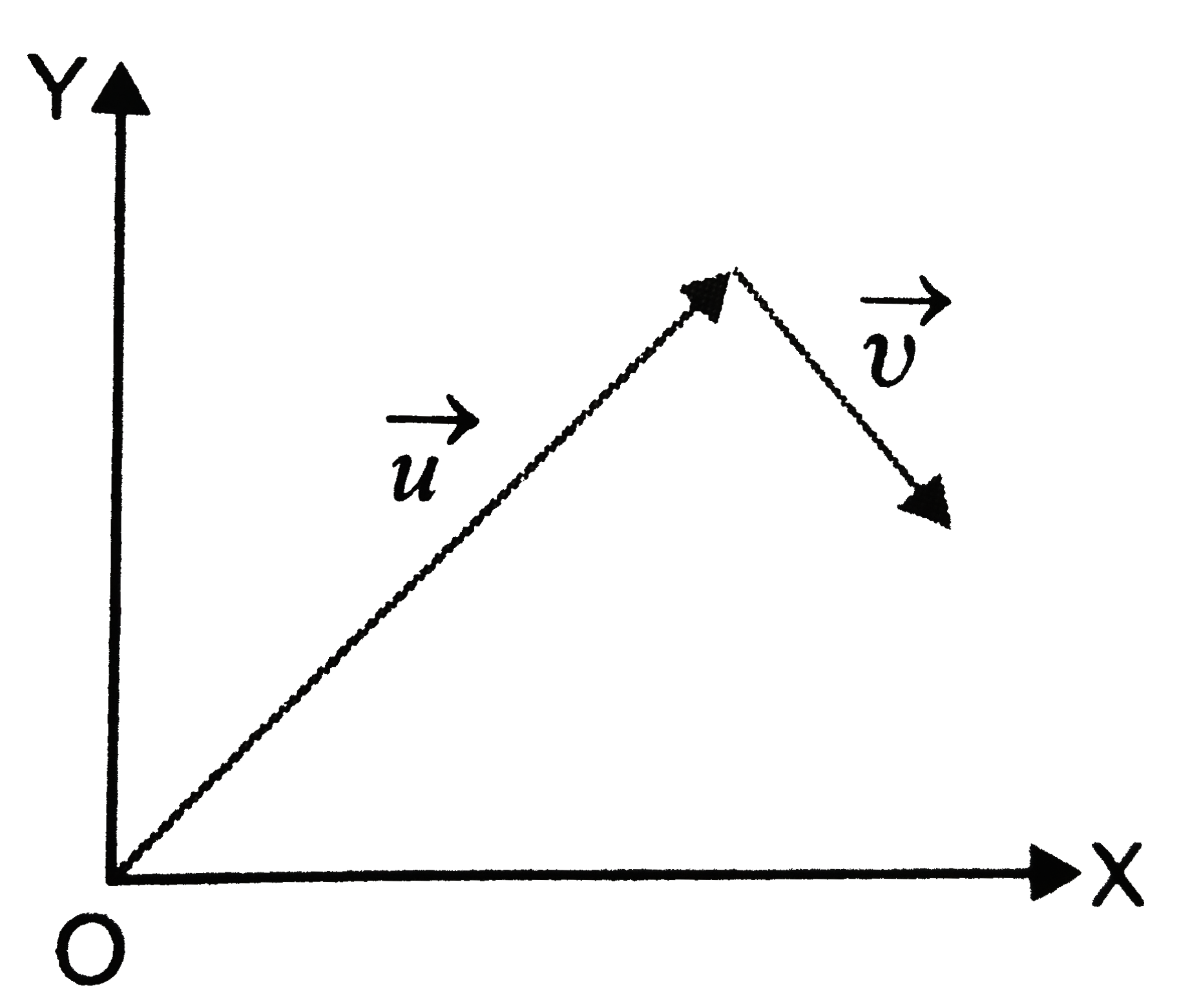
Figure shows the orientation of two vectors $\to u$ and $\to v$ in the (XY) plane.
If $\to u = a ˆ i + b ˆ j$ and $\to v = p ˆ i + q ˆ j$ which of the following is correct ?
.

A

a and p are positive while b and q are negative

B

a, p and b are positive while q is negative

C

a, q and b are positive while p is negative

D

a, b, p and q are all positive

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Clearly from the diagram, $u = a ˆ i + b ˆ j$
As u is in the first quadrant, hence both components a and b will be positive.
For $v = p ˆ i + q ˆ j$ , as it is in positive x-direction and located downward hence x-component p will be positive and y-component q will be negative.

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Figure 2 (EP). 13 shows the orientatione of two vectors $\to u$ and $\to v$ in the (XY) plane.
If $\to u = a ˆ I + b ˆ j$ and $\to v = p ˆ + q ˆ j$ which of the following is correct ?
.
A(a) $a$ and $p$ are psoitive while $b$ and $q$ are negative
B(b) $a, q$ and $b$ are positve while $q$ is negative
C(c ) $a, b, q$ and $b$ positve whicl $p$ is negative
D(d) $a, b, p$ and $q$ are all positive
Question 2 - Select One
Let $\to u = ˆ i - ˆ j, \to v = 2 ˆ i + 5 ˆ j, \to w = 4 ˆ i + 3 ˆ j and \to p = \to u + \to v + \to w$ . Which one of the following is correct ?
A $- 3 \to u + 2 \to v = \to p$
B $3 \to u - 2 \to v = \to p$
C $3 \to u + 2 \to v = \to p$
D $- 3 \to u - 2 \to v = \to p$

NCERT EXEMPLAR-MOTION IN A PLANE-Multiple Choice Questions

Home
Ask Doubt
Profile