The area of a trapezium is half the product of its height and the sum of parallel sides. GIVEN : A trapezium ABCD in which ABCD;AB=a,DC=b and AL=CM=h, where AL⊥DC and CM⊥AB. TO PROVE : ar(trap.ABCD)=12HX(A+B) construction : Join AC
area of trapezium ABCD=area of ∠ABC+ area of ∠ACB
=12⋅AB⋅h+12⋅DC⋅h
=12⋅h⋅(AB+CD)
=12⋅h(a+b).
Topper's Solved these Questions
Similar Questions
The area of a parallelogram is the product of its base and the corresponding altitude. GIVEN : A parallelogram ABCD in which AB is the base and AL the corresponding altitude. TO PROVE : ar(^(gm)ABCD)=ABxAL CONSTRUCTION : Complete the rectangle ALMB by drawing BM⊥CD.
View SolutionShow that the sum of the three altitudes of a triangle is less than the sum of three sides of the triangle. GIVEN : A ABC in which AD⊥BC,BE⊥AC and CF⊥AB. PROVE : AD+BE+CF<AB+BC+AC
View SolutionThe area of a triangle is half the product of any of its sides and the corresponding altitude. GIVEN : A ABC in which AL is the altitude to the side BC. TO PROVE : ar(ABC)=12(BC×AL) CONSTRUCTION : Through C and A draw CDBA and ADBC respectively, intersecting each other at D.
View SolutionShow that a median of a triangle divides it into two triangles of equal area. GIVEN : A ABC in which AD is the median. TO PROVE : ar(ABD)=ar(ADC) CONSTRUCTION : Draw AL⊥BC
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).
 View Solution
View SolutionABCD is a trapezium with ABDC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : (i) Quadrilateral EFGH is a parallelogram ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join AC and HF
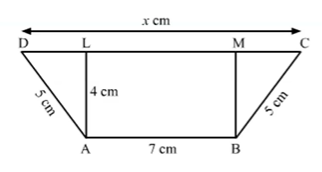
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
 View Solution
View SolutionABCD is a trapezium with AB∣∣DC . A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionABCD is a trapezium in which ABDC. If ar(ABD)=24 cm2and AB=8 cm, then height of ABC is 3 cm (b) 4 cm (c) 6 cm (d) 8 cm
View Solution

