ABCD is a parallelogram. E is a point on BA such that BE=2EA and F is a point on Do such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third area of parallelogram ABCD
Given: BE=2EA and DF=2FC
To Prove: ar(∥gmAECF)=13ar(∥gmABCD)
Proof: BE=2EA and DF=2FC
⇒AB−AE=2AE and DC−FC=2FC
⇒AB=3AE and DC=3FC
⇒AE=13AB and FC=13DC
⇒AE=FC [AB=DC]
∴AEFC is a parallelogram.
Clearly, parallelogram ABCD and AEFC have the same altitude and AE=13AB.
ar(∥gmAECF)=h×13AB=13×h×AB=13ar(∥gmABCD)
∴ar(∥gmAECF)=13ar(∥gmABCD)
Hence Proved.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram. E is a point on BA such that BE=2EA and F is a point on Do such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third area of parallelogram AB CD
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2 EA and F is a point on DC such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third of the area of parallelogram AB CD.
View Solution
Knowledge Check
- Question 1 - Select One
In the figure, the area of parallelogram ABCD is
 AAB×BMBBC×BNCDC×DLDAD×DL
AAB×BMBBC×BNCDC×DLDAD×DL
ABCD is a parallelogram. P is a point on AD such that AP=13AD and Q is a point on BC such that CQ=13BP . Prove that AQCP is a parallelogram.
View SolutionD, E, F are the mid points of side AB, BC, AC prove that BDEF is a parallelogram whose area is half that of Δ ABC
View SolutionABCD is a parallelogram. E is a point on BC such that BE : EC = m:n. If AE and DB intersect in F, then what is the ratio of the area of triangle FEB to the area of triangle AFD?
View SolutionIn the given figure, ABCD is a parallelogram whose area is 60cm2. Find the area of ΔACB
 View Solution
View SolutionThe area of any parallelogram ABCD, is AB X BC.
View SolutionIn the adjoining figure, find the area of the parallelogram ABCD.
 View Solution
View SolutionIn the adjoining figure, prove that ABCD is a parallelogram. Also find its area.
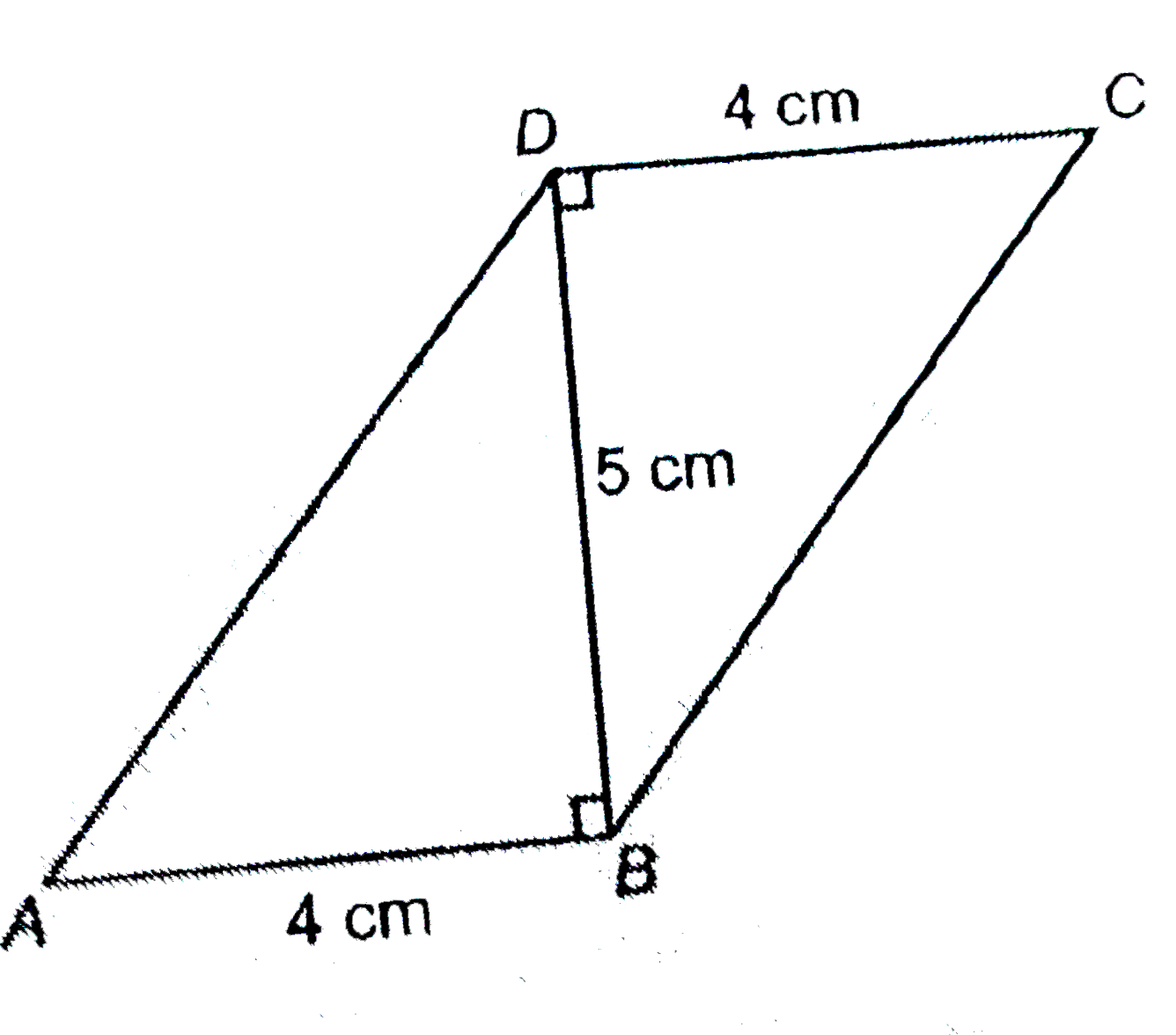 View Solution
View Solution

