In above problem, if coefficient of friction for both the spheres is same and let t1 and t2 be the times when pure rolling of solid sphere and of hollow sphere is started. Then :
t1=t2
t1<t2
t1>t2
None of these
The correct Answer is:B
Friction force μ mg acts in forward direction till pure rolling is started. Hence, linear acceleration
a=μmgm=μg∴v=at or t=va=ω0μg(1R+mRI)
Again Isolid<Ihollow∴tsolid<thollow or t1<t2
Similar Questions
In the above problem, if coefficient of friction for both the spheres is same and let t1 and t2 be the times when pure rolling of solid sphere and of hollow sphere is started. Then
View SolutionAssertion : A solid and a hollow sphere both of equal masses and radii are put on a rough surface after rotating with some angular velocity say ω0. Coefficient of friction for both the spheres and ground is same. Solid sphere will start pure rolling first
Reason : Radius of gyration of hollow sphere about an axis passing through its centre of mass is more.View Solution
Knowledge Check
- Question 1 - Select One
In the above problem, if coefficient of friction for both the spheres is same and let t1 and t2 be the times when pure rolling of solid sphere and of hollow sphere is started. Then
At1=t2Bt1<t2Ct1>t2DNone of these - Question 2 - Select One
Assertion : A solid and a hollow sphere both of equal masses and radii are put on a rough surface after rotating with some angular velocity say ω0. Coefficient of friction for both the spheres and ground is same. Solid sphere will start pure rolling first
Reason : Radius of gyration of hollow sphere about an axis passing through its centre of mass is more.AIf both Assertion and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are true but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is fasleDIf Assertion is false but Reason is true - Question 3 - Select One
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.Aω20r281μgB227ω20r2μgC481ω20r2μgD281ω20r281μg
Solve the above problem if thickness of the hollow sphere is considerable.
 View Solution
View SolutionSolve the above problem if thickness of the hollow sphere is considerable.
 View Solution
View SolutionA solid sphere of radius R is set into motion on a rough horizontal surface with a linear speed v0 in forward direction and an angular with a linear speed v0 in forward direction and an angular velocity ω0=v0/2R in counter clockwise direction as shown in figure. If coefficient of friction μ then find
a. the time after which sphere starts pure rolling,
b. the linear speed of sphere when it starts rolling and
c. the work down by friction over a long time.
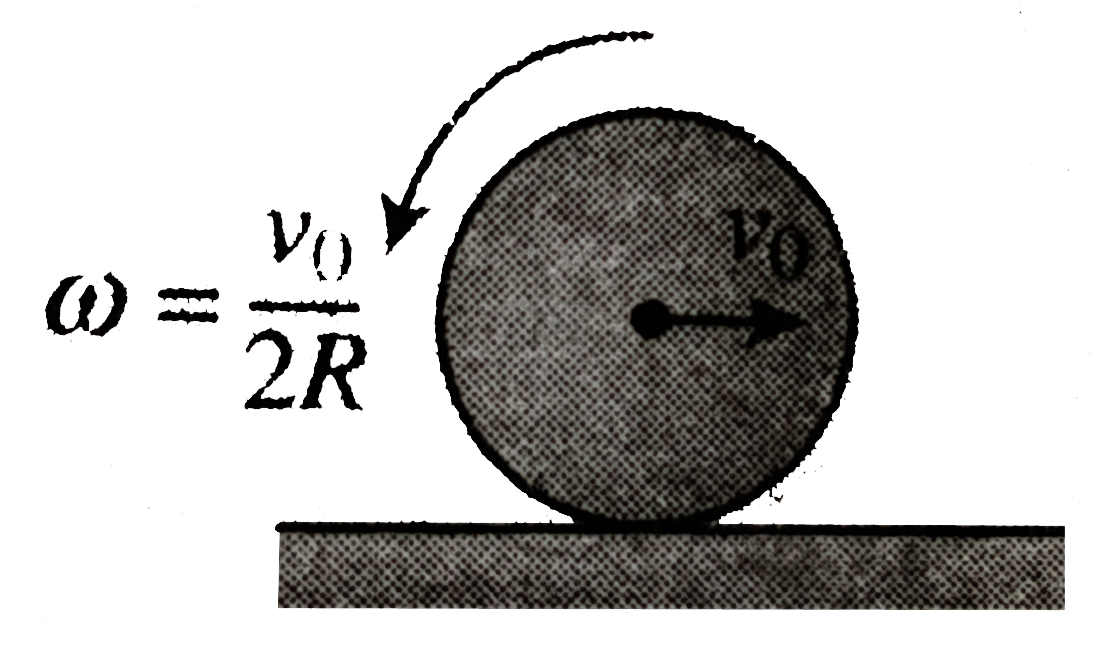 View Solution
View SolutionA solid sphere of radius R is set into motion on a rough horizontal surface with a inear speed v0 in forward direction and an angular with a linear speed v0 in forward directioin and an angular velocity ω0=v0/2R in counter clockwise direction as shown in figure. If coefficient of friction μ then find
a. the time after which sphere starts pure rolling,
b. the linear speed of sphere when it starts rolling and
c. the work down by friction over a long time.
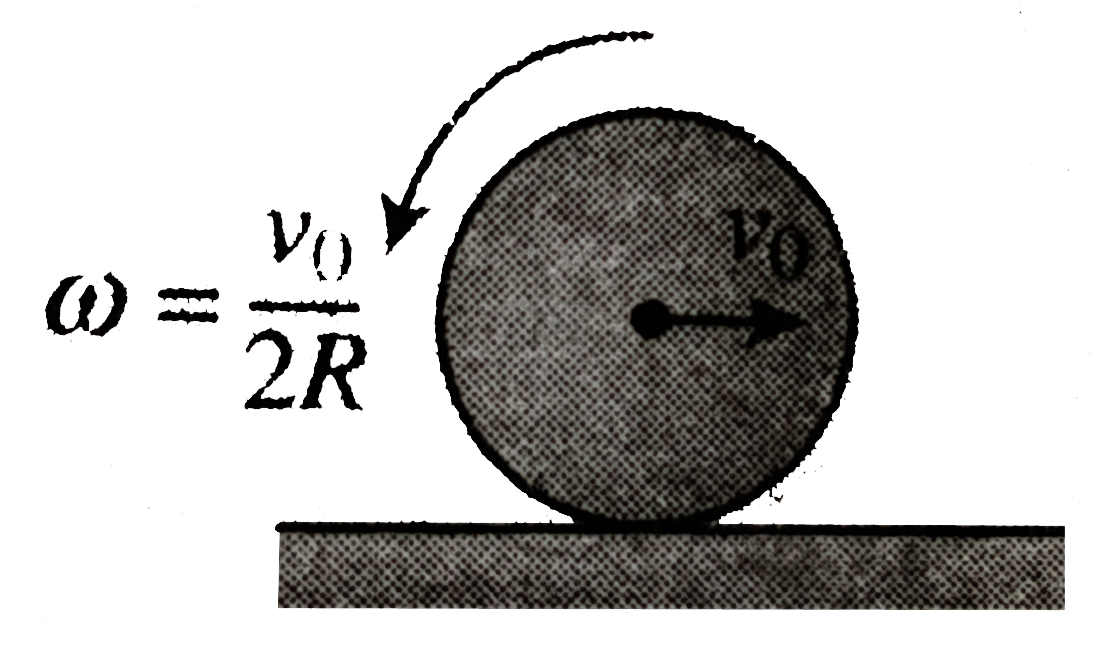 View Solution
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the velocity of the sphere after the pure rolling startsView Solution

