In the above problem, if coefficient of friction for both the spheres is same and let t1 and t2 be the times when pure rolling of solid sphere and of hollow sphere is started. Then
t1=t2
t1<t2
t1>t2
None of these
The correct Answer is:B
To solve the problem, we need to analyze the motion of both the solid sphere and the hollow sphere under the influence of friction until they start pure rolling. We will derive the expressions for the times T1 and T2 for the solid and hollow spheres respectively.
1. Understanding the Forces Acting on the Spheres:
- Both spheres experience a frictional force due to the coefficient of friction μ. This force acts in the forward direction and is given by Ff=μmg, where m is the mass of the sphere and g is the acceleration due to gravity.
2. Linear Acceleration:
- The linear acceleration a of the spheres can be expressed as:
a=Ffm=μmgm=μg
3. Angular Acceleration:
- The angular acceleration α for both spheres is related to the linear acceleration by the equation:
α=ar
- For the solid sphere, the moment of inertia I is 25mr2, and for the hollow sphere, it is 23mr2.
4. Relating Linear and Angular Motion:
- The relationship between linear and angular motion leads to:
τ=Iα
- The torque τ due to friction is τ=Ff⋅r=μmg⋅r.
5. Finding Time for Pure Rolling:
- For the solid sphere:
μmg⋅r=25mr2⋅α⟹α=5μg2r
- For the hollow sphere:
μmg⋅r=23mr2⋅α⟹α=3μg2r
6. Calculating Time T1 and T2:
- The time taken for the solid sphere to start pure rolling T1:
T1=va=rω0μg=r⋅5μg2rμg=52μg
- The time taken for the hollow sphere to start pure rolling T2:
T2=va=rω0μg=r⋅3μg2rμg=32μg
7. Comparing T1 and T2:
- Since T1=52μg and T2=32μg, we can conclude:
T1<T2
Conclusion:
Thus, the time when pure rolling starts for the solid sphere T1 is less than the time for the hollow sphere T2. Therefore, T1<T2.
- Both spheres experience a frictional force due to the coefficient of friction μ. This force acts in the forward direction and is given by Ff=μmg, where m is the mass of the sphere and g is the acceleration due to gravity.
- The linear acceleration a of the spheres can be expressed as:
a=Ffm=μmgm=μg
- The angular acceleration α for both spheres is related to the linear acceleration by the equation:
α=ar
- For the solid sphere, the moment of inertia I is 25mr2, and for the hollow sphere, it is 23mr2.
- The relationship between linear and angular motion leads to:
τ=Iα
- The torque τ due to friction is τ=Ff⋅r=μmg⋅r.
- For the solid sphere:
μmg⋅r=25mr2⋅α⟹α=5μg2r
- For the hollow sphere:
μmg⋅r=23mr2⋅α⟹α=3μg2r
- The time taken for the solid sphere to start pure rolling T1:
T1=va=rω0μg=r⋅5μg2rμg=52μg
- The time taken for the hollow sphere to start pure rolling T2:
T2=va=rω0μg=r⋅3μg2rμg=32μg
- Since T1=52μg and T2=32μg, we can conclude:
T1<T2
Thus, the time when pure rolling starts for the solid sphere T1 is less than the time for the hollow sphere T2. Therefore, T1<T2.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
Solve the above problem if thickness of the hollow sphere is considerable.

View SolutionAssertion : A solid and a hollow sphere both of equal masses and radii are put on a rough surface after rotating with some angular velocity say ω0. Coefficient of friction for both the spheres and ground is same. Solid sphere will start pure rolling first
Reason : Radius of gyration of hollow sphere about an axis passing through its centre of mass is more.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
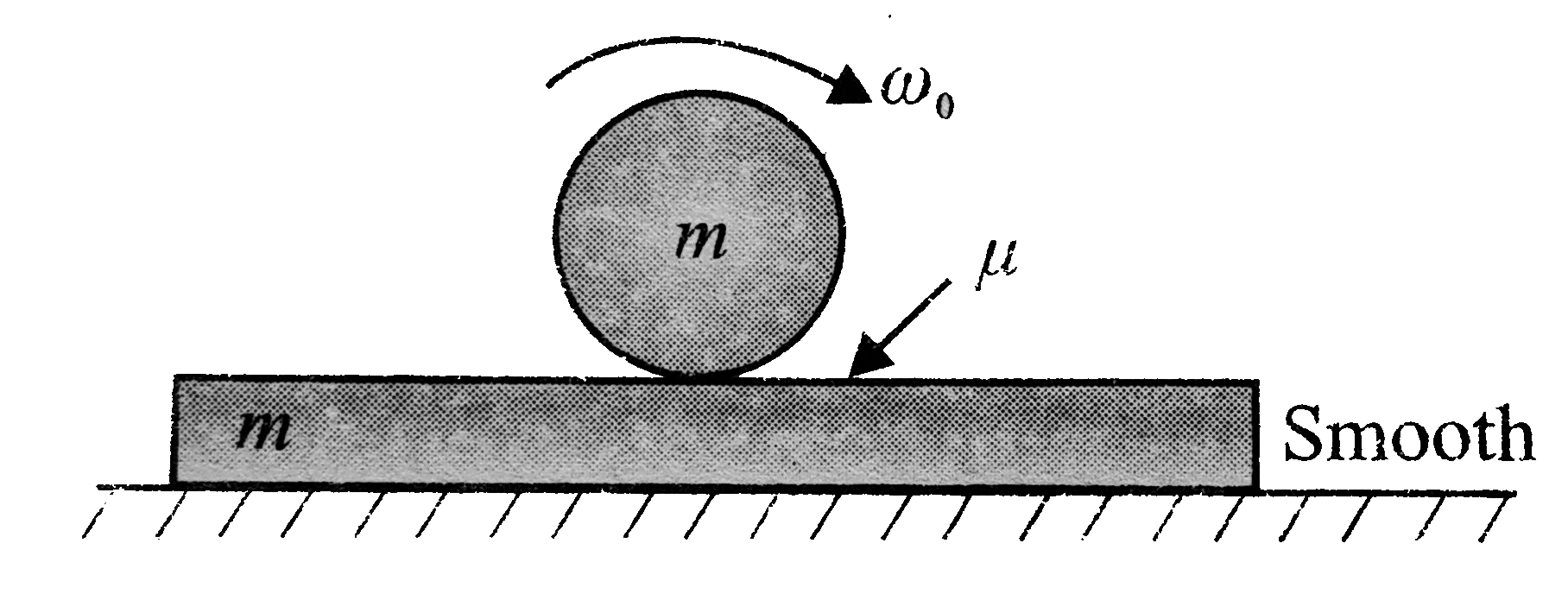
Find the time t at which the pure roiling starts
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
View SolutionIf a solid and a hollow conducting sphere have same radius then
View SolutionA solid sphere of radius R is set into motion on a rough horizontal surface with a inear speed v0 in forward direction and an angular with a linear speed v0 in forward directioin and an angular velocity ω0=v0/2R in counter clockwise direction as shown in figure. If coefficient of friction μ then find
a. the time after which sphere starts pure rolling,
b. the linear speed of sphere when it starts rolling and
c. the work down by friction over a long time.
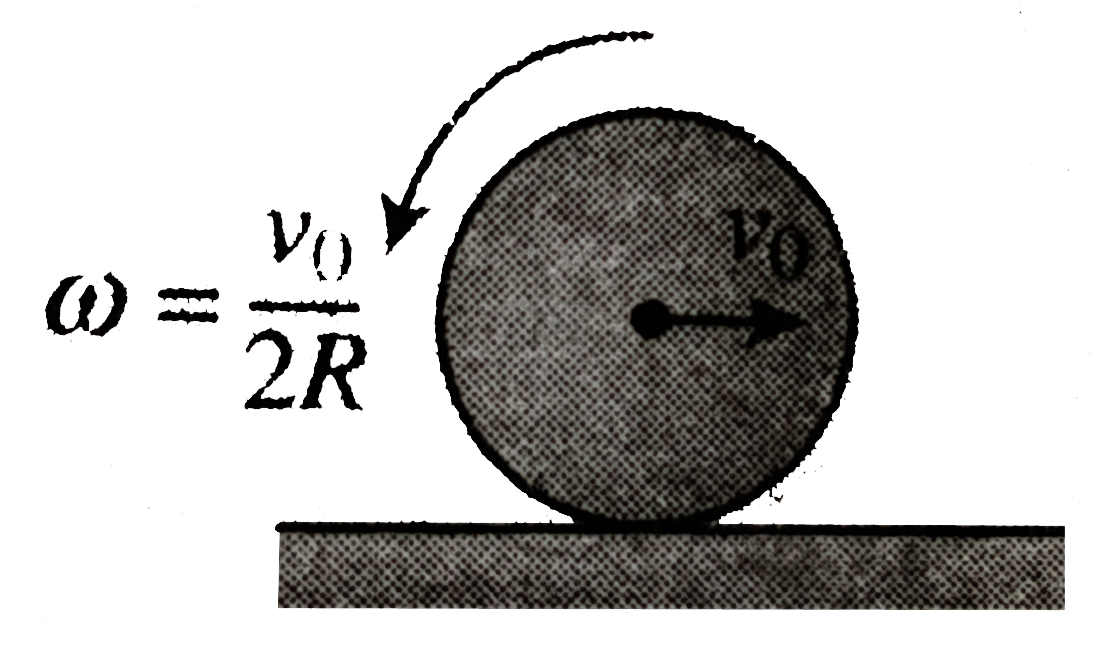
View SolutionLength AB in the figure shown in 5 m. The body is released from A. Friction is sufficient for pure rolling to take place.

In the above case suppose we have four bodies ring, disc, solid sphere and hollow sphere. The angle θ is now gradually increased. Which body will start slipping very fast. All the bodies have same mass and radius. Coefficient of friction is also same ?
View Solution
A solid sphere of mass m and radius R is gently placed on a conveyer belt moving with constant velocity v0. If coefficient of friction between belt and sphere is 2/7 the distance traveled by the centre of the sphere before it starts pure rolling is
View SolutionA solid and a hollow sphere are released from the top of a sufficiently rough inclined plane. The solid sphere has same mass but its radius is half of the radius of hollow sphere. Both are performing pure rolling Which of the following statements is correct regarding their kinetic energy when they reach at the bottom of plane? (K = Kinetic energy)
View SolutionA solid sphere is in pure rolling motion on an inclined surface having inclination θ
View Solution