Out of a disc of mass M and radius R a concentric disc of mass m and radius r is removed. The M.I. of the remaining part about the symmetric axis will be :
(M−m)(R+r)2/2
(M−m)(R2−r2)/2
(M−m)(R−r)2/2
(M−m)(R2+r2)/2
The correct Answer is:D
To solve the problem of finding the moment of inertia (M.I.) of the remaining part of a disc after removing a concentric disc, we can follow these steps:
Step 1: Understand the Problem
We have a larger disc of mass M and radius R. From this disc, we remove a smaller concentric disc of mass m and radius r. We need to find the moment of inertia of the remaining part about the symmetric axis.
Step 2: Moment of Inertia of the Whole Disc
The moment of inertia I of a solid disc about its central axis is given by the formula:
I=12MR2
For the larger disc, this will be:
I1=12MR2
Step 3: Moment of Inertia of the Removed Disc
For the smaller disc that is removed, its moment of inertia about the same axis is:
I2=12mr2
Step 4: Calculate the Moment of Inertia of the Remaining Part
The moment of inertia of the remaining part after removing the smaller disc can be calculated using the principle of subtraction:
I=I1−I2
Substituting the values we found:
I=12MR2−12mr2
Step 5: Factor Out Common Terms
We can factor out 12:
I=12(MR2−mr2)
Step 6: Relate Masses and Densities
Since all discs are made of the same material, we can relate the masses and areas using density σ. The mass of the larger disc is:
M=σ⋅πR2
And for the smaller disc:
m=σ⋅πr2
Thus, the remaining mass after removing the smaller disc is:
M−m=σ⋅π(R2−r2)
Step 7: Substitute Back into the Moment of Inertia Equation
Now we can substitute M and m back into our equation for I:
I=12(σ⋅πR2R2−σ⋅πr2r2)
This simplifies to:
I=σ⋅π2(R4−r4)
Final Result
Thus, the moment of inertia of the remaining part about the symmetric axis is:
I=12(MR2−mr2)
We have a larger disc of mass M and radius R. From this disc, we remove a smaller concentric disc of mass m and radius r. We need to find the moment of inertia of the remaining part about the symmetric axis.
The moment of inertia I of a solid disc about its central axis is given by the formula:
I=12MR2
For the larger disc, this will be:
I1=12MR2
For the smaller disc that is removed, its moment of inertia about the same axis is:
I2=12mr2
The moment of inertia of the remaining part after removing the smaller disc can be calculated using the principle of subtraction:
I=I1−I2
Substituting the values we found:
I=12MR2−12mr2
We can factor out 12:
I=12(MR2−mr2)
Since all discs are made of the same material, we can relate the masses and areas using density σ. The mass of the larger disc is:
M=σ⋅πR2
And for the smaller disc:
m=σ⋅πr2
Thus, the remaining mass after removing the smaller disc is:
M−m=σ⋅π(R2−r2)
Now we can substitute M and m back into our equation for I:
I=12(σ⋅πR2R2−σ⋅πr2r2)
This simplifies to:
I=σ⋅π2(R4−r4)
Thus, the moment of inertia of the remaining part about the symmetric axis is:
I=12(MR2−mr2)
Similar Questions
From a disc of radius r1, a concentric disc of radius r2 is removed . The mass of the remaining portion is m. Find the M.I. of the remaining about an axis passing through the center of mass and perpendicular to the plane.
View SolutionFrom a circular disc of radius R, another disc of diameter R is removed. Locate c.m. of the remaining portion.

View Solution
Knowledge Check
From a circular disc of mass M and radius R, a part of 60∘ is removed. The M.I. of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is
 A56MR2B53MR2C512MR2D524MR2
A56MR2B53MR2C512MR2D524MR2A disc of radius r is removed from the centre of a disc of mass M and radius R. The M.I. About the axis through the centre and normal to the plane will be:
AM(R2−r2)/2BM(R2+r2)/2CM(R4−r4)/2R2DM(R2)/2Form a circular disc of radius R and mass 9M , a small disc of mass M and radius R/3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the the plane of the disc and passing its centre is :-
AMR2B4MR2C49MR2D409MR2
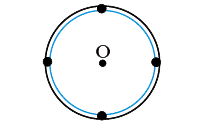
Four similar point masses (each of mass m) are placed on the circumference of a disc of mass M and radius R. The M.I. of the system about the normal axis through the centre O will be:
View SolutionFrom a semicircular disc of radius r1, another semicircular disc of radius r2 is removed. Find the c.m. of the remaining position.

View SolutionA rectangular piece of dimension l×b is cut out of central portion of a uniform circular disc of mass m and radius r. The moment of inertia of the remaining piece about an axis perpendicular to the plane of the disc and passing through its centre is :
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of mass M and radius R3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is
View SolutionMoment of inertia of a disc of mass 'M' and radius 'R' about the diameter is
View Solution
