A disc of radius r is removed from the centre of a disc of mass M and radius R. The M.I. About the axis through the centre and normal to the plane will be:
M(R2−r2)/2
M(R2+r2)/2
M(R4−r4)/2R2
M(R2)/2
The correct Answer is:B
To find the moment of inertia of a disc with a smaller disc removed from its center, we can follow these steps:
Step 1: Moment of Inertia of the Whole Disc
The moment of inertia I of a solid disc of mass M and radius R about an axis through its center and normal to its plane is given by the formula:
I=12MR2
Step 2: Moment of Inertia of the Smaller Disc
Next, we need to find the moment of inertia of the smaller disc that is being removed. Let the radius of the smaller disc be r and its mass be m′. The mass m′ can be calculated using the area density of the larger disc. The area of the larger disc is πR2 and the area of the smaller disc is πr2. The mass per unit area σ of the larger disc is:
σ=MπR2
Thus, the mass m′ of the smaller disc is:
m′=σ⋅Area of smaller disc=MπR2⋅πr2=Mr2R2
The moment of inertia I′ of the smaller disc about the same axis is given by:
I′=12m′r2=12(Mr2R2)r2=12Mr4R2
Step 3: Net Moment of Inertia After Removing the Smaller Disc
The net moment of inertia Inet after removing the smaller disc from the larger disc is:
Inet=I−I′=12MR2−12Mr4R2
Factoring out 12M:
Inet=12M(R2−r4R2)
To combine the terms, we can write:
Inet=12M(R4−r4R2)
Final Result
Thus, the moment of inertia about the axis through the center and normal to the plane after removing the smaller disc is:
Inet=M2⋅R4−r4R2
The moment of inertia I of a solid disc of mass M and radius R about an axis through its center and normal to its plane is given by the formula:
I=12MR2
Next, we need to find the moment of inertia of the smaller disc that is being removed. Let the radius of the smaller disc be r and its mass be m′. The mass m′ can be calculated using the area density of the larger disc. The area of the larger disc is πR2 and the area of the smaller disc is πr2. The mass per unit area σ of the larger disc is:
σ=MπR2
Thus, the mass m′ of the smaller disc is:
m′=σ⋅Area of smaller disc=MπR2⋅πr2=Mr2R2
I′=12m′r2=12(Mr2R2)r2=12Mr4R2
The net moment of inertia Inet after removing the smaller disc from the larger disc is:
Inet=I−I′=12MR2−12Mr4R2
Factoring out 12M:
Inet=12M(R2−r4R2)
To combine the terms, we can write:
Inet=12M(R4−r4R2)
Thus, the moment of inertia about the axis through the center and normal to the plane after removing the smaller disc is:
Inet=M2⋅R4−r4R2
Similar Questions
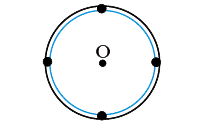
Four similar point masses (each of mass m) are placed on the circumference of a disc of mass M and radius R. The M.I. of the system about the normal axis through the centre O will be:
 View Solution
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View Solution
Knowledge Check
- Question 1 - Select One
The moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
 AMR22B7MR212C7MR26D5MR212
AMR22B7MR212C7MR26D5MR212 - Question 2 - Select One
A solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π=22/7 and √149=12.2)
AR3BR2CR6DR4 - Question 3 - Select One
Four similar point masses (m each) are symmetrically placed on the circumference of a disc of mass M and radius R. Moment of inertia of the system about an axis passing through centre O and perpendicular to the plane of the disc will be
AMR2+4mR2BMR2+85mR2CmR2+4MR2DMR22+4mR2
Calculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionFour particles, each of mass m, are lying symmetrically on the rim of a disc of mass M and radius R. M.I. of this system about an axis passing through one of the particles and perpendicular to plane of disc is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is αR from the centre of the bigger disc . the value of α is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is αR from the centre of the bigger disc . the value of α is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the cirucmferences of the discs coincide. The centre of mass of the new disc is αR from the center of the bigger disc. The value of α is
View Solution

