At constant temperature if a graph plotted between logP and has an intercept of unity then what will be the value of constant (k)
1
10
100
1000
The correct Answer is:B
To solve the problem step by step, we will analyze the relationship between pressure (P) and volume (V) of a gas at constant temperature and derive the value of the constant k.
Step 1: Understand the relationship between P and V
For a fixed amount of gas at constant temperature, we know from Boyle's Law that pressure (P) is inversely proportional to volume (V). This can be expressed mathematically as:
P∝1V
This means that:
P=k⋅1V
where k is a constant.
Step 2: Take the logarithm of both sides
Now, we take the logarithm of both sides of the equation:
logP=logk+log(1V)
Using the property of logarithms that states log(1V)=−logV, we can rewrite the equation as:
logP=logk−logV
Step 3: Rearranging the equation
Rearranging the equation gives us:
logP+logV=logk
or
logP=−logV+logk
This is in the form of a linear equation y=mx+c, where:
- y=logP
- m=−1 (the slope)
- x=logV
- c=logk (the y-intercept)
Step 4: Analyze the graph
According to the problem, the graph plotted between logP and log(1V) has an intercept of unity. This means:
logk=1
Step 5: Solve for k
To find k, we convert the logarithmic form back to its exponential form:
k=101=10
Final Answer
Thus, the value of the constant k is:
10
---
For a fixed amount of gas at constant temperature, we know from Boyle's Law that pressure (P) is inversely proportional to volume (V). This can be expressed mathematically as:
P∝1V
This means that:
P=k⋅1V
where k is a constant.
Now, we take the logarithm of both sides of the equation:
logP=logk+log(1V)
Using the property of logarithms that states log(1V)=−logV, we can rewrite the equation as:
logP=logk−logV
Rearranging the equation gives us:
logP+logV=logk
or
logP=−logV+logk
This is in the form of a linear equation y=mx+c, where:
- y=logP
- m=−1 (the slope)
- x=logV
- c=logk (the y-intercept)
According to the problem, the graph plotted between logP and log(1V) has an intercept of unity. This means:
logk=1
To find k, we convert the logarithmic form back to its exponential form:
k=101=10
Thus, the value of the constant k is:
10
Similar Questions
Knowledge Check
Under constant temperature, graph between P and 1/V is a
AparabolaBhyperbolaCstraight lineDcircleA graph plotted between log k vs 1T is represented by
A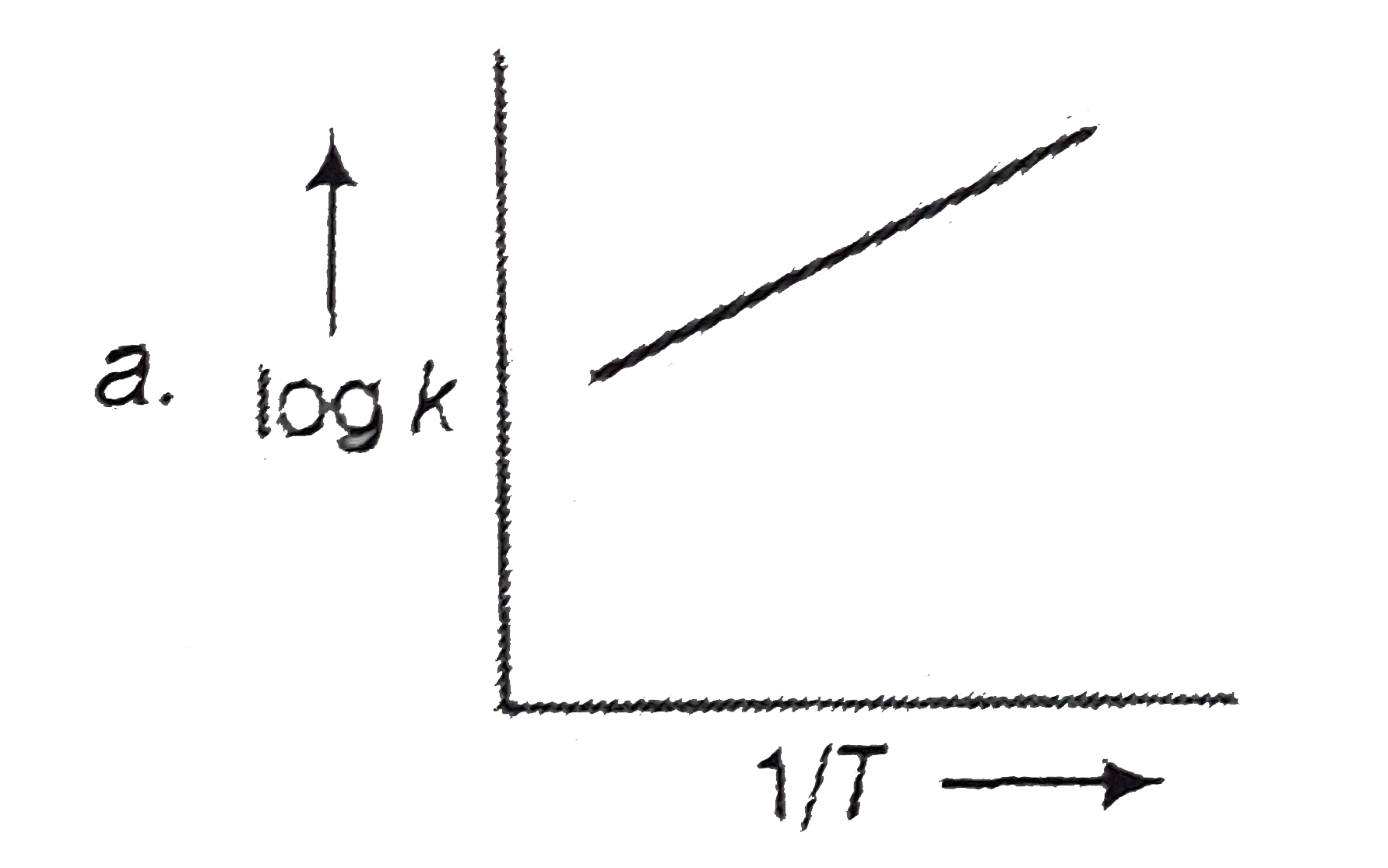 B
B C
C D
D
A graph plotted between log N vs, time gives a slope and intercept equal to:
A−λ2.303,logN0Bλ2.303,logN0C−λ2.303,N0Dλ2.303,N0
What is the type of graph that would result between log(V) and log(1T) at constant pressure?
View SolutionWhen a plot between logk and 1/T is plotted we get the graph as shown.
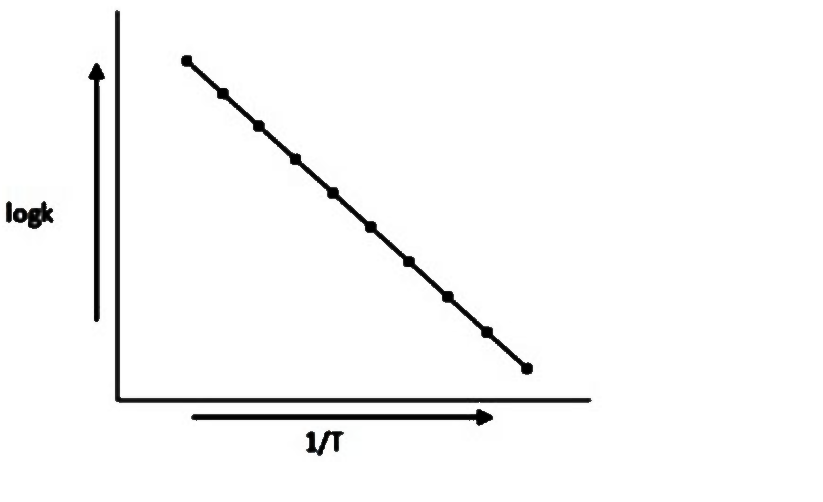
What is the value of slope in the graph?
View SolutionFor sperical mirros graph plotted between −1V and −1uis .
View SolutionUnder constant pressure, graph between p and 1V is a
View SolutionIf we plot a graph between log K and 1T by Arrhenius equation , the slope is
View Solution
