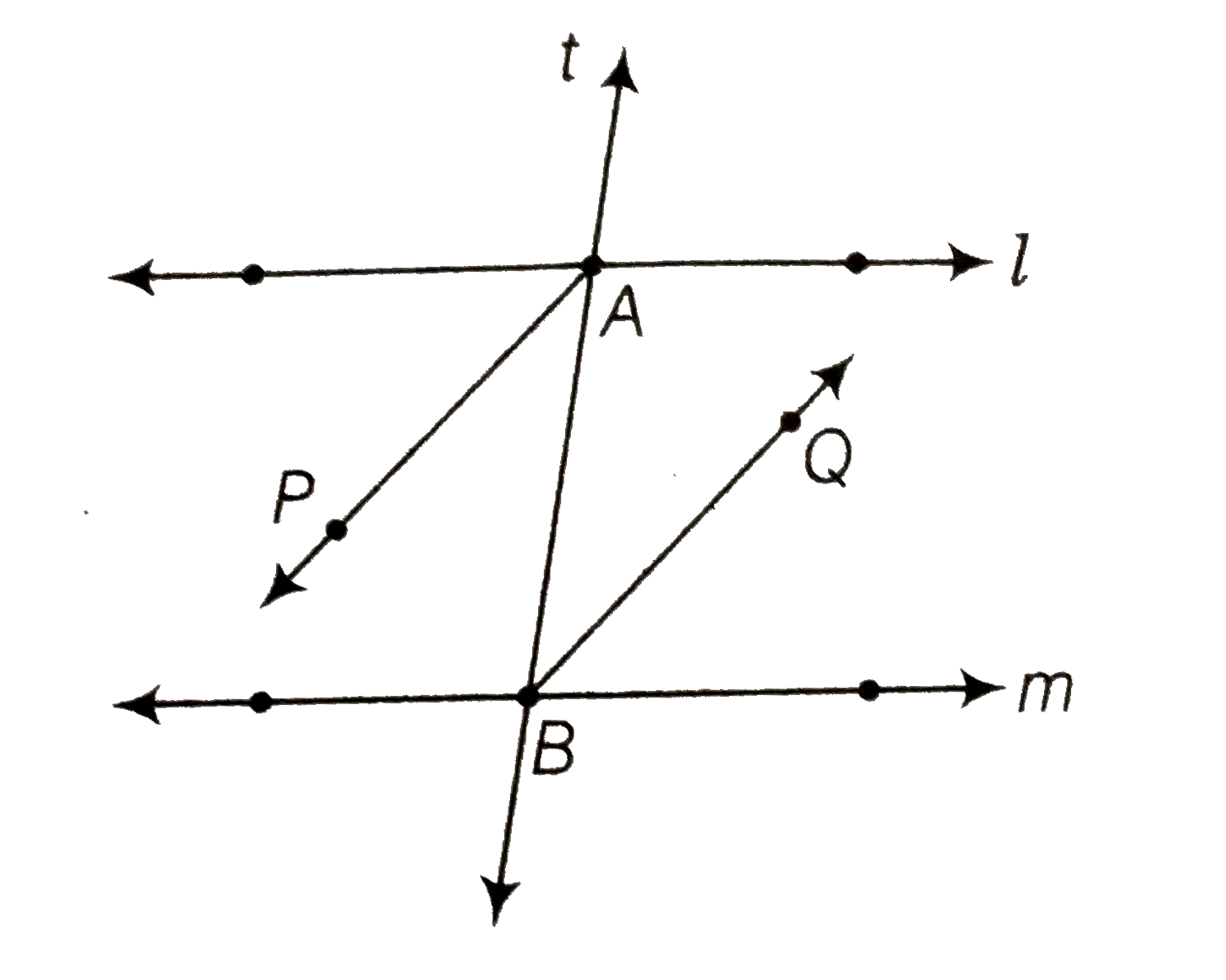
In the given figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l m.
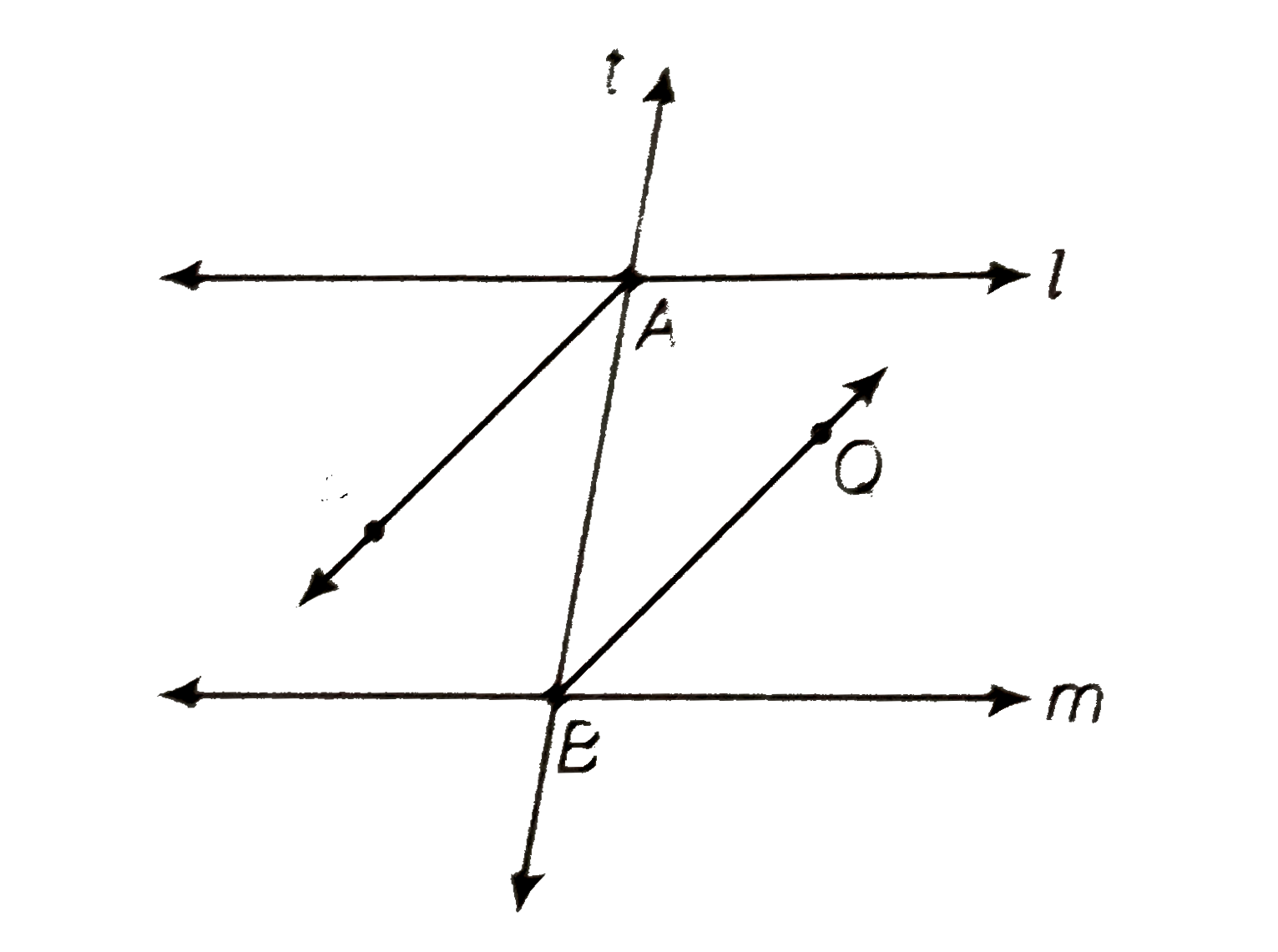
Given. In the figure AP BQ, AP and BQ are the bisectors of alternate interior angles
ABF
To show lm
proof Since, AP BQ and t is transversal, therefore [alternate interior angles ]
[multiplying both sides by 2]
ABF
So, alternate interior angles are equal.
We know that, if two alternate interior angles are equal, then lines are parallel.
Hence, lm
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If two parallel lines are cut by a transversal, then the alternate interior angles are equal
ATRUEBFALSECCannot be determinedDNone of these
In the given figure, name the point in the interior of angle: (a) POQ (b) QORView SolutionIf two parallel lines are intersected by a transversal then prove that the bisectors of any pair of alternate interior angles are parallel.
View SolutionIn the given figure, AC>AB and AD is the bisector of ∠A. show that ∠ADC>∠ADB.
 View Solution
View Solution.In the given figure,if exterior angle is 105∘ and the interior opposite angles are equal.Find ∠A and ∠C
View SolutionAP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given figure). Show that AP||BQ.
 View Solution
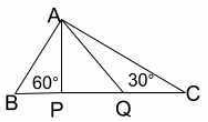
View SolutionIn the given figure, AP is perpendicular to BC, and AQ is the bisector ∠PAC. What will be the measure of ∠PAQ?
 View Solution
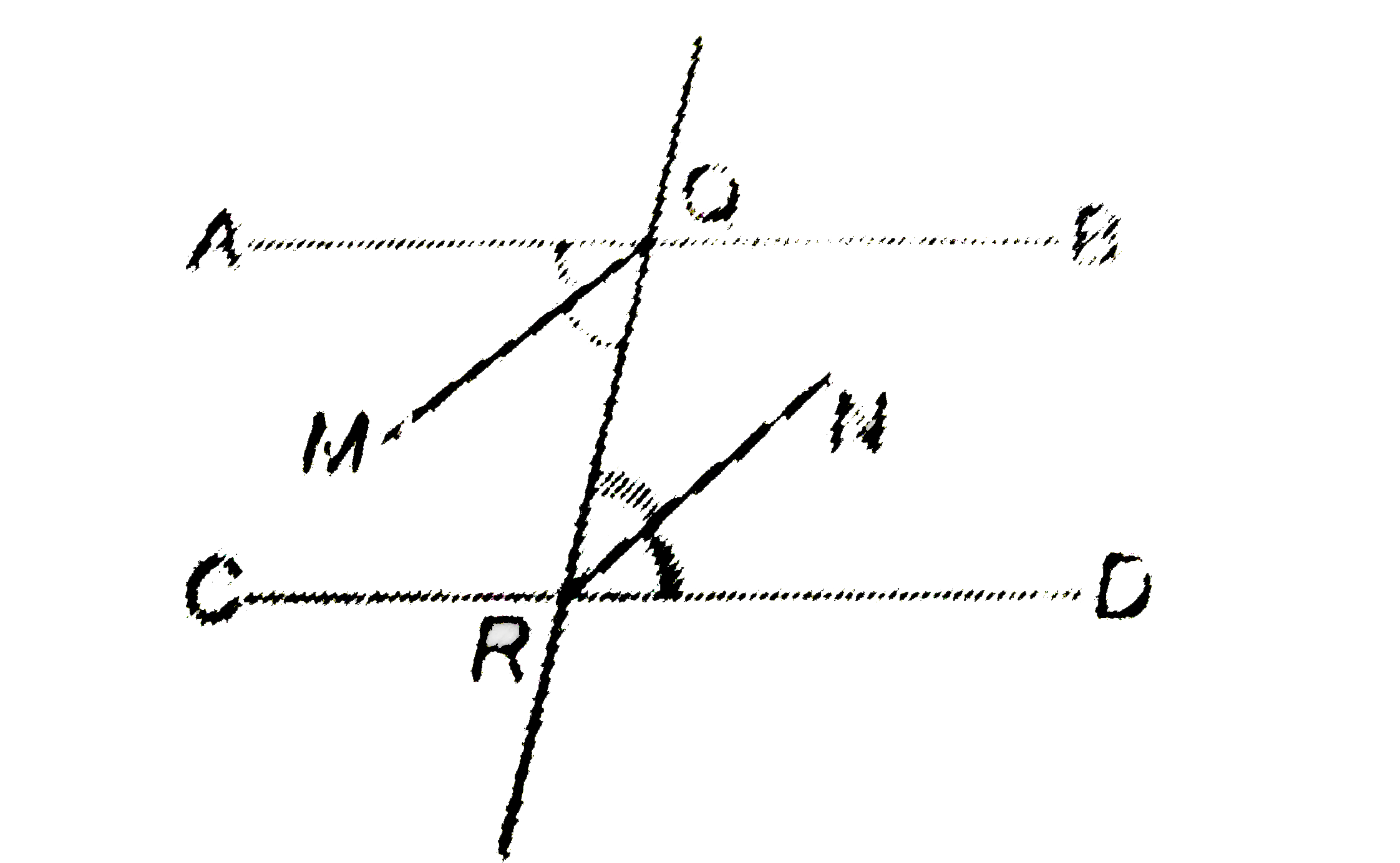
View SolutionIn the following figure, AB||CD, QM and RN are bisectors of alternate angles AQR and QRD respectively. Show that QM||RN.
 View Solution
View Solution


