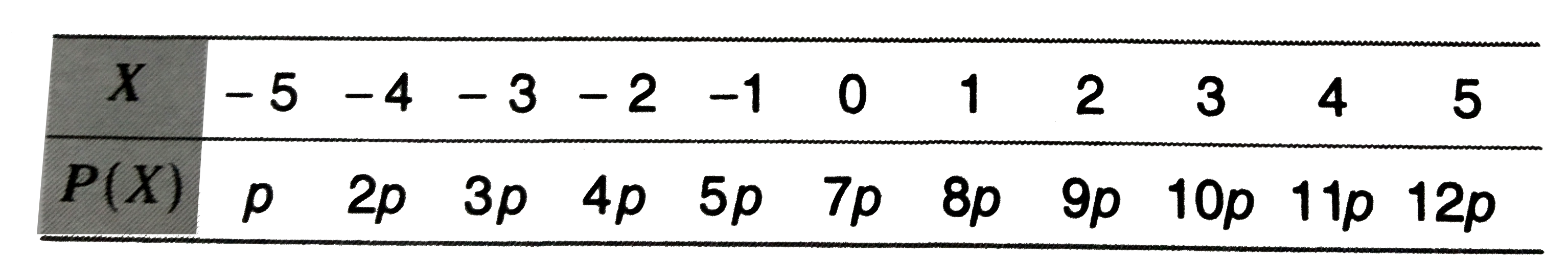A probability distribution of a variable X is given below: X:01234 P(X):0.10.250.30.20.15 Find (i) Var(X) (ii) Var(X2)
Video Solution
Text Solution
var(x)=E(X2)−(E(X))2
∑PiX2i−(∑PiXi)2
∑PiX2i=0.(0.1)2+1(0.25)+22(0.3)+32(0.2)+42(0.15)
0.25+1.2+1.8+2.4
=5.65
∑PiXi=0X0.1+(1)(0.25)+2(0.3)+3(0.2)+4(0.15)
0+0.25+0.6+0.6+0.6
2.05
Var(x)=5.65+(2.05)2=1.44
Therefore, Var(X)=a2var(X)
Var(x2)=(12)2X1.44
0.361
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The probability distribution of a discrete random variable X is given below
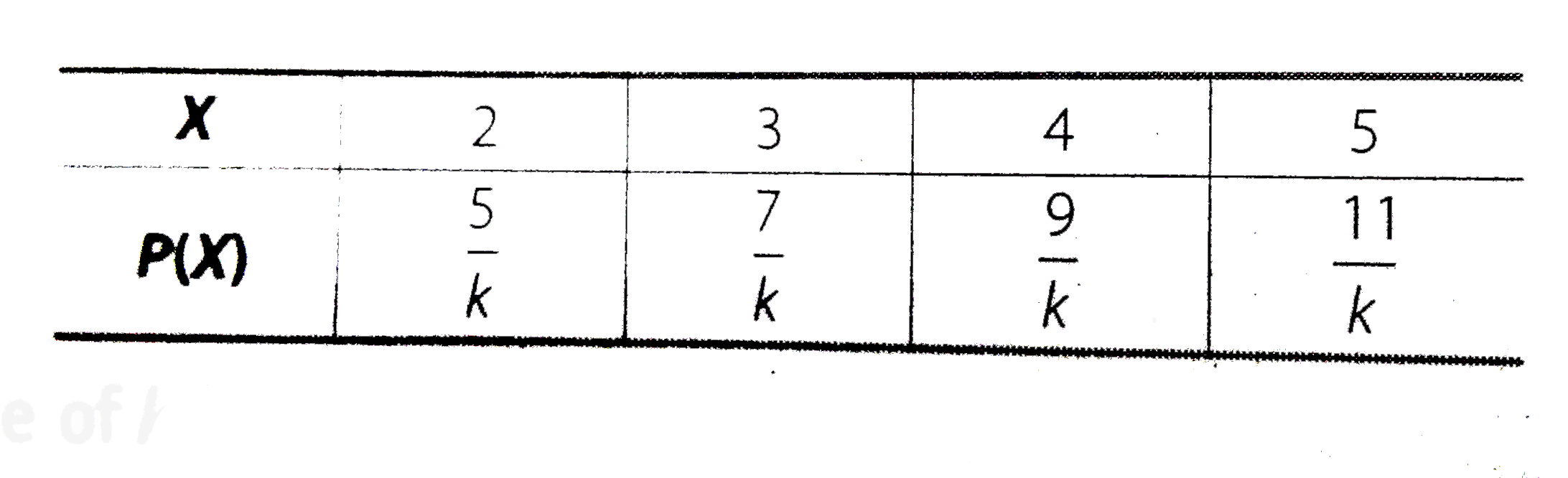
The value of k isA8B16C32D48 - Question 2 - Select One
The probability distribution of a random variable X is given by.
X=x:01234P(X=x):0.40.30.10.10.1
The variance of X, isA1.76B2.45C3.2D4.8
The probability distribution of the random variable X is given by
Then, the value of V(X) is equal to
 View Solution
View SolutionIf the probability distribution of a random variable X is as given below: X=xi: 1 2 3 4 P(X=xi): c 2c 3c 4c Write the value of P(X≤2) .
View SolutionIf the probability distribution of a random variable X is as given below
Then, mean and variance are
 View Solution
View SolutionThe probability of a random variable X is given below
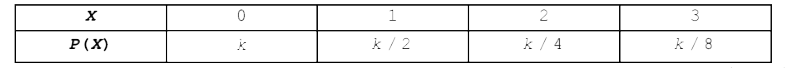
Find P(X≤2)+P(X>2)View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionThe probability distribution of a random variable x is given below: What is the standard deviation of x?
View Solution