A beg (mass M) hangs by a long thred and a bullet (mass m) comes horizontally with velocity v and gets caught in the bag. The for the combined (bag+bullet) system -
Momentum is mvM(M+m)
KE is mv22
Momentum is mv(M+m)M
KE is m2v22(M+m)
The correct Answer is:D
To solve the problem, we need to analyze the situation using the principles of conservation of momentum and kinetic energy. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the System
We have a bag of mass M hanging by a thread and a bullet of mass m coming horizontally with a velocity v. When the bullet gets caught in the bag, we need to analyze the combined system of the bag and the bullet.
Step 2: Apply Conservation of Momentum
Before the collision, only the bullet has momentum. The initial momentum p1 of the system is given by:
p1=m⋅v
After the bullet gets caught in the bag, the total mass of the system becomes M+m. Let V be the final velocity of the combined system after the bullet is caught. By conservation of momentum:
Initial Momentum=Final Momentum
Thus, we have:
m⋅v=(M+m)⋅V
Step 3: Solve for Final Velocity V
Rearranging the equation from Step 2 to find V:
V=m⋅vM+m
Step 4: Calculate Final Kinetic Energy
The initial kinetic energy KEinitial of the bullet is:
KEinitial=12mv2
After the bullet is caught in the bag, the kinetic energy KEfinal of the combined system is:
KEfinal=12(M+m)V2
Substituting V from Step 3:
KEfinal=12(M+m)(m⋅vM+m)2
This simplifies to:
KEfinal=12(M+m)⋅m2v2(M+m)2=m2v22(M+m)
Step 5: Conclusion
From the calculations, we have derived the final velocity V and the final kinetic energy KEfinal of the combined system.
Summary of Results
- Final Velocity V=m⋅vM+m
- Final Kinetic Energy KEfinal=m2v22(M+m)
We have a bag of mass M hanging by a thread and a bullet of mass m coming horizontally with a velocity v. When the bullet gets caught in the bag, we need to analyze the combined system of the bag and the bullet.
Before the collision, only the bullet has momentum. The initial momentum p1 of the system is given by:
p1=m⋅v
After the bullet gets caught in the bag, the total mass of the system becomes M+m. Let V be the final velocity of the combined system after the bullet is caught. By conservation of momentum:
Initial Momentum=Final Momentum
Thus, we have:
m⋅v=(M+m)⋅V
Rearranging the equation from Step 2 to find V:
V=m⋅vM+m
The initial kinetic energy KEinitial of the bullet is:
KEinitial=12mv2
After the bullet is caught in the bag, the kinetic energy KEfinal of the combined system is:
KEfinal=12(M+m)V2
Substituting V from Step 3:
KEfinal=12(M+m)(m⋅vM+m)2
This simplifies to:
KEfinal=12(M+m)⋅m2v2(M+m)2=m2v22(M+m)
From the calculations, we have derived the final velocity V and the final kinetic energy KEfinal of the combined system.
- Final Velocity V=m⋅vM+m
- Final Kinetic Energy KEfinal=m2v22(M+m)
Topper's Solved these Questions
Similar Questions
A wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.

View SolutionA wooden log of mass M and length L is hinged by a frictionless nail at O. A bullet of mass m strikes with velocity v and sticks to it. Find the angular velocity of the system, immediately after the collision about O. Also, calculate the minimum value of v so that log becomes horizontal after collision.
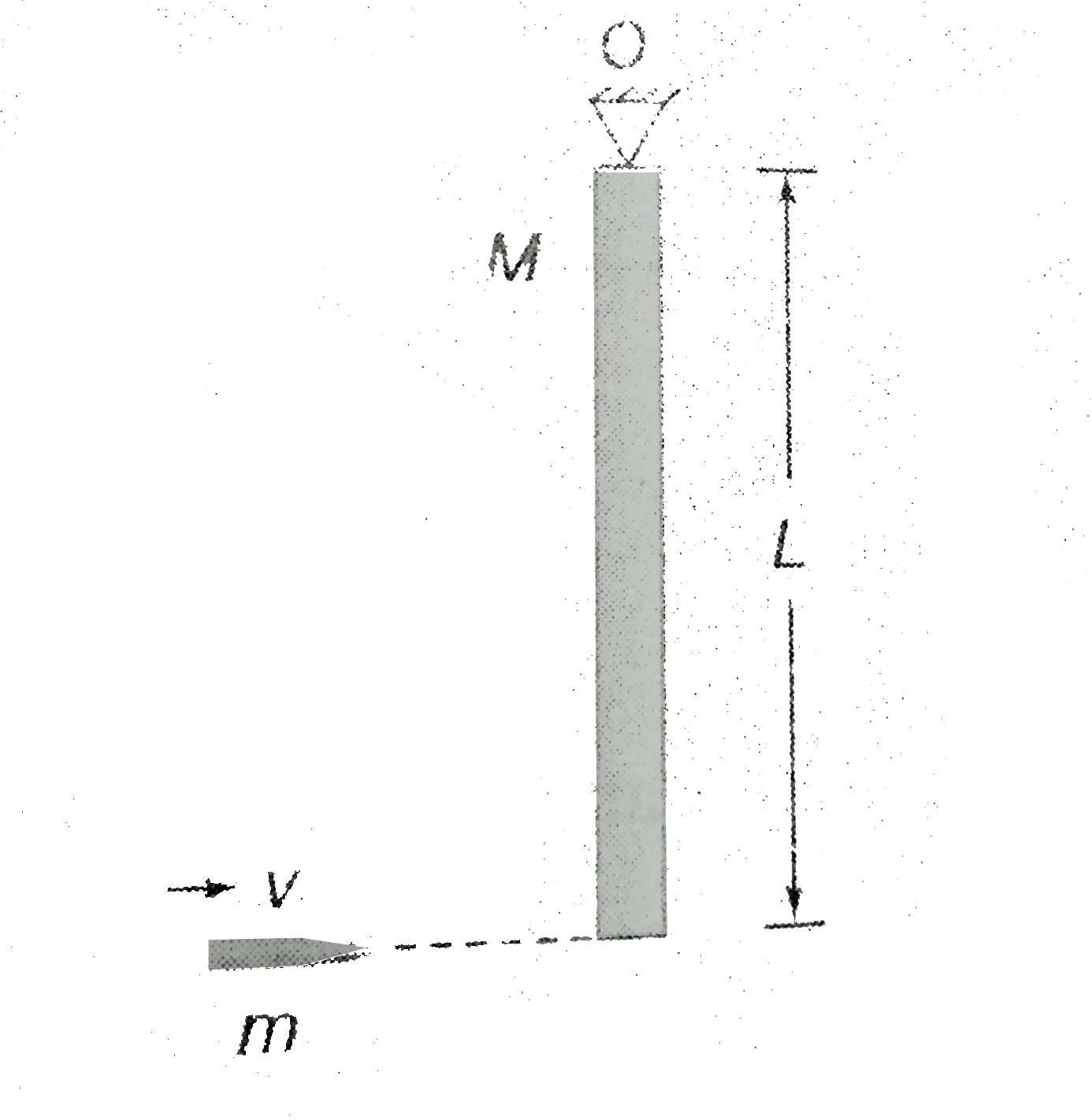
View Solution
Knowledge Check
A bag (mass M) hangs by a long thred and a bullet (mass m) comes horizontally with velocity v and gets caught in the bag. Then for the combined (bag+bullet) system -
AMomentum is mvMM+mBKinetic energy is mv22CMomentum is mv(M+m)MDKinetic energy is m2v22(M+m)A bag (mass M) hangs by a long thred and a bullet (mass m) comes horizontally with velocity v and gets caught in the bag. Then for the combined (bag+bullet) system -
AMomentum is (mMv)/(M+m)BKinetic energy is 12Mv2CMomentum ismv(M+m)MDKinetic energy ism2v22(M+m)A bag of mass M hangs by a long massless rope. A bullet of mass in, moving horizontally with velocity u, is caught in the bag. Then for the combined (bag + bullet) system, just after collision
Amomentum is muM/(M+m)Bkinetic energy is mu2/2Cmomentum is mu(M+m)/MDkinetic energy is m2u2/2(M+m)
A bag of sand of mass m is suspended by a rope. A bullet of mass m20 is fired at it with a velocity vand gets embedded into it. The velocity of the bag finally is
View SolutionA bag of sand of mass M is suspended by a string. A bullet of mass m is fired at it with velocity v and gets embedded into it. The loss of kinetic energy in this process is
View SolutionA wooden block of mass M rests on a horizontal surface. A bullet of mass m moving in the horizontal direction strikes and gets embedded in it. The combined system covers a distance x on the surface. If the coefficient of friction between wood and the surface is μ , the speed of the bullet at the time of striking the block is (where m is mass of the bullet)
View SolutionA bullet of mass m is fired with velocity v in a large bulk of mass M. The final velocity v' will be
View SolutionA bullet of mass m is fired with velocity v in a large bulk of mass M. The final velocity v' will be
View Solution
