A uniform metal dise of radius R is taken and out of it a disc of diameter R is cut off from the end. The centre of the mass of the remaining part will be:
R4from the centre
R3from the centre
R5 from the centre
R6 from the centre
The correct Answer is:D
To find the center of mass of the remaining part of a uniform metal disk after cutting out a smaller disk, we can follow these steps:
Step 1: Understand the Problem
We have a uniform disk of radius R and we cut out a smaller disk of diameter R (which means its radius is R2). We need to find the center of mass of the remaining part.
Step 2: Calculate the Mass of the Original Disk
The mass of the original disk can be expressed as:
M=σ⋅A
where σ is the density and A is the area of the disk. The area of the original disk is:
A=πR2
Thus, the mass of the original disk is:
M=σ⋅πR2
Step 3: Calculate the Mass of the Cut-Out Disk
The area of the cut-out disk (with radius R2) is:
Acut=π(R2)2=πR24
The mass of the cut-out disk is:
Mcut=σ⋅Acut=σ⋅πR24
Step 4: Determine the Center of Mass of the Cut-Out Disk
The center of mass of the cut-out disk is located at a distance R2 from the center of the original disk.
Step 5: Apply the Center of Mass Formula
We can treat the remaining part as a combination of the original disk and a negative mass for the cut-out disk. The center of mass xcm can be calculated using the formula:
xcm=M⋅0−Mcut⋅R2M−Mcut
Substituting the values we have:
xcm=M⋅0−(σ⋅πR24)⋅R2M−Mcut
Step 6: Simplify the Expression
Substituting M=σ⋅πR2 and Mcut=σ⋅πR24:
xcm=0−(σ⋅πR24)⋅R2σ⋅πR2−σ⋅πR24
This simplifies to:
xcm=−σ⋅πR38σ⋅πR2(1−14)=−R83R24=−R6
Step 7: Conclusion
The center of mass of the remaining part is located at a distance of R6 from the center of the original disk, in the opposite direction of the cut-out disk.
Final Answer:
The center of mass of the remaining part will be R6 away from the center of the original disk, in the direction opposite to the cut-out disk.
---
We have a uniform disk of radius R and we cut out a smaller disk of diameter R (which means its radius is R2). We need to find the center of mass of the remaining part.
The mass of the original disk can be expressed as:
M=σ⋅A
where σ is the density and A is the area of the disk. The area of the original disk is:
A=πR2
Thus, the mass of the original disk is:
M=σ⋅πR2
The area of the cut-out disk (with radius R2) is:
Acut=π(R2)2=πR24
The mass of the cut-out disk is:
Mcut=σ⋅Acut=σ⋅πR24
The center of mass of the cut-out disk is located at a distance R2 from the center of the original disk.
We can treat the remaining part as a combination of the original disk and a negative mass for the cut-out disk. The center of mass xcm can be calculated using the formula:
xcm=M⋅0−Mcut⋅R2M−Mcut
Substituting the values we have:
xcm=M⋅0−(σ⋅πR24)⋅R2M−Mcut
Substituting M=σ⋅πR2 and Mcut=σ⋅πR24:
xcm=0−(σ⋅πR24)⋅R2σ⋅πR2−σ⋅πR24
This simplifies to:
xcm=−σ⋅πR38σ⋅πR2(1−14)=−R83R24=−R6
The center of mass of the remaining part is located at a distance of R6 from the center of the original disk, in the opposite direction of the cut-out disk.
The center of mass of the remaining part will be R6 away from the center of the original disk, in the direction opposite to the cut-out disk.
Topper's Solved these Questions
Similar Questions
A thin homogeneous lamina is in the form of a circular disc of radius R. From it a circular hole exactly hall the radius of the lamina and touching the lamina's circumference is cut off. Find the centre of mass of the remaining part.
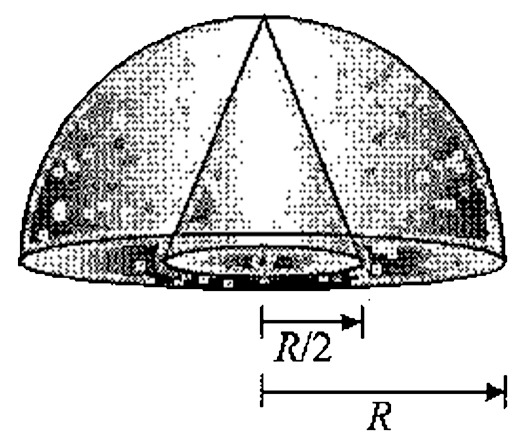
View SolutionFrom a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.
View Solution
Knowledge Check
A uniform metal disc of radius R is taken and out of it a disc of diameter R is cut-off from the end. The center of mass of the remaining part will be
AR4 from the centerBR3 from the centerCR5 from the centerDR6 from the center.A uniform sphere has radius R. A sphere of diameter R is cut from its edge as shown. Then the distance of centre of mass of remaining portion from the centre of mass of the original sphere is
 AR/7BR/14C2R/7DR/18
AR/7BR/14C2R/7DR/18A disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
Ar5Br4Cr2Dr3
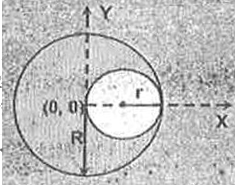
A disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion

View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionFrom the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at

View SolutionFrom a disc of radius R and mass m, a circular hole of diamter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
View SolutionA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View Solution
