If net flux through a Caussian surface is zero, then find whether the following statements are correct or not.
There are no changes inside the surface.
To determine whether the statement "There are no charges inside the surface" is correct when the net flux through a Gaussian surface is zero, we can analyze the situation using Gauss's Law.
1. Understanding Gauss's Law:
Gauss's Law states that the electric flux (Φ) through a closed surface is proportional to the net charge (Q_enc) enclosed by that surface. Mathematically, it is expressed as:
Φ=Qencε0
where ε0 is the permittivity of free space.
2. Analyzing Zero Flux:
If the net flux through the Gaussian surface is zero, then according to Gauss's Law:
Φ=0⟹Qenc=0
This means that the total charge enclosed by the Gaussian surface is zero.
3. Implications of Zero Charge:
The statement "There are no charges inside the surface" can be misleading. While it is true that the net charge is zero, it does not necessarily mean that there are no charges present. For example:
- There could be a positive charge +Q and a negative charge −Q inside the surface, which would result in a net charge of zero.
- There could also be multiple charges that balance each other out, leading to a net charge of zero.
4. Conclusion:
Therefore, the statement "There are no charges inside the surface" is not necessarily correct. It is possible to have charges inside the surface that cancel each other out, resulting in a net charge of zero and thus zero flux.
Final Answer:
The statement is incorrect. There can be charges inside the surface that balance each other out, leading to a net charge of zero.
---
Gauss's Law states that the electric flux (Φ) through a closed surface is proportional to the net charge (Q_enc) enclosed by that surface. Mathematically, it is expressed as:
Φ=Qencε0
where ε0 is the permittivity of free space.
If the net flux through the Gaussian surface is zero, then according to Gauss's Law:
Φ=0⟹Qenc=0
This means that the total charge enclosed by the Gaussian surface is zero.
The statement "There are no charges inside the surface" can be misleading. While it is true that the net charge is zero, it does not necessarily mean that there are no charges present. For example:
- There could be a positive charge +Q and a negative charge −Q inside the surface, which would result in a net charge of zero.
- There could also be multiple charges that balance each other out, leading to a net charge of zero.
Therefore, the statement "There are no charges inside the surface" is not necessarily correct. It is possible to have charges inside the surface that cancel each other out, resulting in a net charge of zero and thus zero flux.
The statement is incorrect. There can be charges inside the surface that balance each other out, leading to a net charge of zero.
Topper's Solved these Questions
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) FILL IN THE BLANKS
4 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL - II & III
15 Videos
- ELECTROSTANTICSBOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - EXERCISE
10 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBOOK - FIITJEECHAPTER - ELECTROMAGNETIC WAVE & WAVE OPTICSEXERCISE - ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
21 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
Similar Questions
If net flux through a Gaussian surface is zero, then find whether the following statements are correct or not.
The net charge inside the surface is zero.
View SolutionIf net flux through a Caussian surface is zero, then find whether the following statements are correct or not.
The number of field lines entering the surface equals to the number of field lines leaving the surface.
View Solution
Knowledge Check
The electric flux through the surface
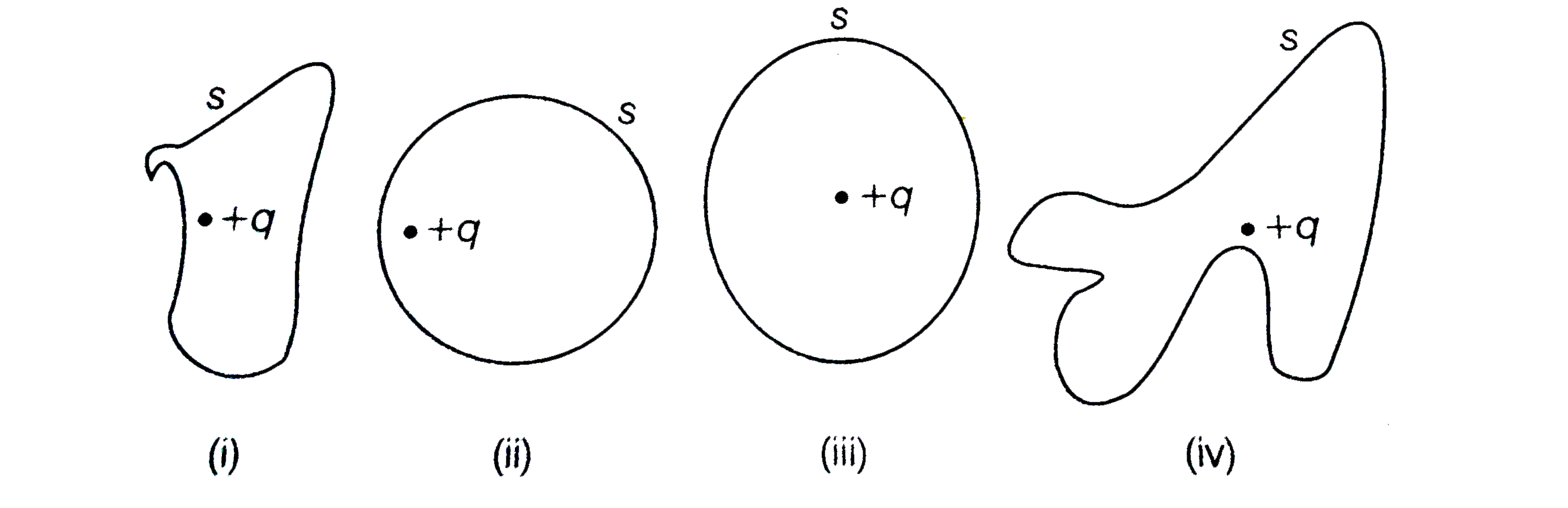 Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.The electric flux through the surface
 Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.
Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.If the net electric flux through a closed surface is zero, then we can infer
Ano net charge is enclosed by the surfaceBuniform electric field exists within the surfaceCelectric potential varies from point to point inside the surfaceDcharge is present inside the surface
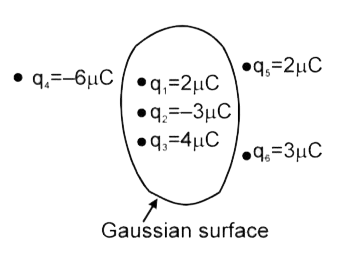
Find out flux through given gaussian surface.
View SolutionIf electric flux passing through a close surface is zero then :-
View SolutionThe electric flux through the surface :
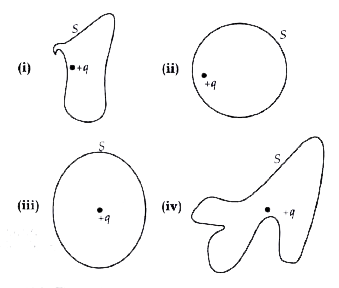
View SolutionFind out flux through the given Gaussian surface.

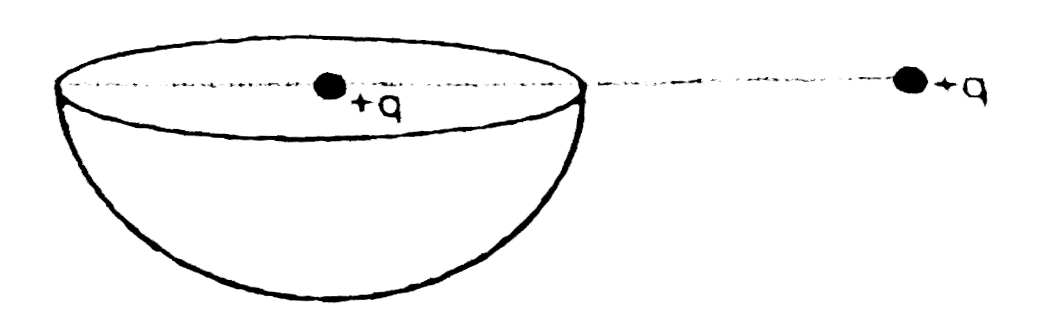
View SolutionFind flux through the hemispherical surface
View Solution
