There are two concentric spherical shells A and B of surface area 20cm2 and 80cm2 . Surfaces ofboth the shells behave like black bodies. It is given thatthethermal conductivity ofmaterial of B is very low and that of A is very high. Initially the temperature of 4 is 400 K and that of B is 300 k. Find the rate of change of temperature of A and B. Given that the heat capacities of A and B are 50J/∘C and 80J/∘C respectively.
To solve the problem step by step, we will use the principles of heat transfer, specifically focusing on radiation and the concept of heat capacity.
Step 1: Understand the Problem
We have two concentric spherical shells, A and B, with given surface areas and temperatures. Shell A has a high thermal conductivity, while shell B has a low thermal conductivity. We need to find the rate of change of temperature for both shells.
Step 2: Identify Given Data
- Surface area of shell A, AA=20cm2=20×10−4m2
- Surface area of shell B, AB=80cm2=80×10−4m2
- Initial temperature of shell A, TA=400K
- Initial temperature of shell B, TB=300K
- Heat capacity of shell A, CA=50J/°C
- Heat capacity of shell B, CB=80J/°C
- Stefan-Boltzmann constant, σ=5.67×10−8W/m2K4
Step 3: Calculate Heat Loss from Shell A
Since shell A has high thermal conductivity, it will primarily radiate heat. The rate of heat loss from shell A can be calculated using the Stefan-Boltzmann law:
dQAdt=AA⋅σ⋅T4A
Substituting the values:
dQAdt=(20×10−4)⋅(5.67×10−8)⋅(400)4
Calculating (400)4:
(400)4=256×108K4
Now substituting this back into the equation:
dQAdt=(20×10−4)⋅(5.67×10−8)⋅(256×108)
Calculating this gives:
dQAdt=2.9J/s
Step 4: Calculate Rate of Change of Temperature for Shell A
Using the formula for the rate of change of temperature:
dTAdt=−1CA⋅dQAdt
Substituting the values:
dTAdt=−150⋅2.9
Calculating this gives:
dTAdt=−0.058K/s
Step 5: Calculate Heat Absorbed by Shell B
Shell B, with low thermal conductivity, absorbs heat from shell A and radiates some heat. The heat absorbed by shell B can be calculated as:
dQBdt=AB⋅σ⋅T4B−dQAdt
Calculating T4B:
(300)4=8.1×108K4
Now substituting into the equation:
dQBdt=(80×10−4)⋅(5.67×10−8)⋅(8.1×108)−2.9
Calculating this gives:
dQBdt=3.67−2.9=0.77J/s
Step 6: Calculate Rate of Change of Temperature for Shell B
Using the formula for the rate of change of temperature:
dTBdt=−1CB⋅dQBdt
Substituting the values:
dTBdt=−180⋅0.77
Calculating this gives:
dTBdt=−0.00963K/s
Final Results
- Rate of change of temperature of shell A: dTAdt=−0.058K/s
- Rate of change of temperature of shell B: dTBdt=−0.00963K/s
We have two concentric spherical shells, A and B, with given surface areas and temperatures. Shell A has a high thermal conductivity, while shell B has a low thermal conductivity. We need to find the rate of change of temperature for both shells.
- Surface area of shell A, AA=20cm2=20×10−4m2
- Surface area of shell B, AB=80cm2=80×10−4m2
- Initial temperature of shell A, TA=400K
- Initial temperature of shell B, TB=300K
- Heat capacity of shell A, CA=50J/°C
- Heat capacity of shell B, CB=80J/°C
- Stefan-Boltzmann constant, σ=5.67×10−8W/m2K4
Since shell A has high thermal conductivity, it will primarily radiate heat. The rate of heat loss from shell A can be calculated using the Stefan-Boltzmann law:
Using the formula for the rate of change of temperature:
Shell B, with low thermal conductivity, absorbs heat from shell A and radiates some heat. The heat absorbed by shell B can be calculated as:
Using the formula for the rate of change of temperature:
- Rate of change of temperature of shell A: dTAdt=−0.058K/s
- Rate of change of temperature of shell B: dTBdt=−0.00963K/s
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.21
1 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.22
1 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.19
1 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
Knowledge Check
A and B are two concentric spherical shells. If A is given a charge +q while B is earthed as shown in figure then
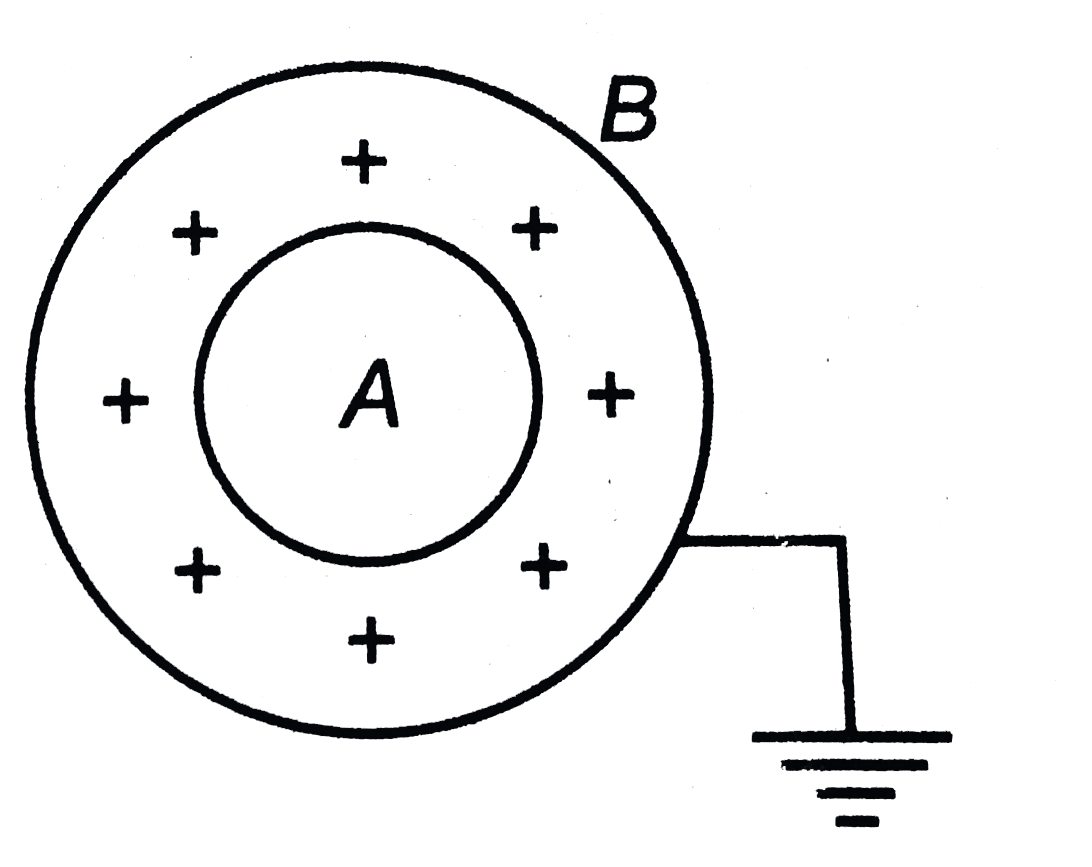 Acharge on the outer surface of shell B is zeroBthe charge on B is equal and opposite to that of ACthe field inside A and outside B is zeroDAll of the above
Acharge on the outer surface of shell B is zeroBthe charge on B is equal and opposite to that of ACthe field inside A and outside B is zeroDAll of the aboveThree concentric metallic spherical shells A,B and C of radii a,band c(a<b<c) have surface charge densities −σ,+σand -sigma respectively,thepotentialofshellA is
A(σ/ε0)[a+b−c]B(σ/ε0)[a−b+c]C(σ/ε0)[b−a−c]Dnone
The radius of a spherical button is increasing at the rate 10cm/sec. Find the rate of change of its surface area when its radius is 4 cm.
View SolutionThe volume of a spherical balloon is increasing at the rate of 20 cm^3/sec . Find the rate of change of its surface area at the instant when radius is 5 cm.
View SolutionA very thin metallic shell of radius r is heated to temperature T and then allowed to cool. The rate of cooling of shell is proportional to
View SolutionThere are two concentric conducting spherical shells of radius rA and rB respectively (rB=2rA). If the inner shell is given a charge Q and outer shell is given a charge 2Q, then the potential difference between the surfaces of the shells will be K=14πε0
View SolutionTwo concentric conducting shells A and B are of radii R and 2R. A charge +q is placed at the centre of the shells. Shell B is earthed and a charge q is given to shell A. Find the charge on outer surface of A and B.
View SolutionFigure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.

View Solution
