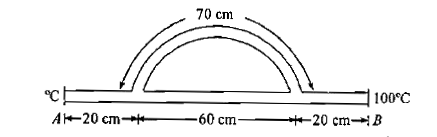
Figure-4.50 shows a thermal network of two metal rods of same cross section area. If the heat current from the ends A and B is 130 W, find the heat current through the curved metal rod.
The correct Answer is:
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Advance MCQs with One or More Option Correct20videos
HEAT TRANSFER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO82videos
HEAT AND THERMAL EXPANSION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO64videos
Kinetic Theory of Gases and Gas Laws
Similar Questions
" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionThe left end of a copper rod (length=20cm, Area of cross section=0.2cm2) is maintained at 20∘C and the right end is maintained at 80∘C . Neglecting any loss of heat through radiation, find (a) the temperature at a point 11cm from the left end and (b) the heat current through the rod. thermal conductivity of copper =385Wm−1C−1 .
View Solution
Knowledge Check
- Question 1 - Select One
A metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKL - Question 2 - Select One
Two rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.
A2πB1πCπDπ2 - Question 3 - Select One
Two rods one is semi circular of thermal conductivity K1 and otheir is straight of thermal conductivity K2 and of same cross sectional area are joined as shown in the The points A and B are maintained at same temperature difference. If rate of flow of heat is same in two rods then K1/K2 is
.A2:πB1:2Cπ:2D3:2
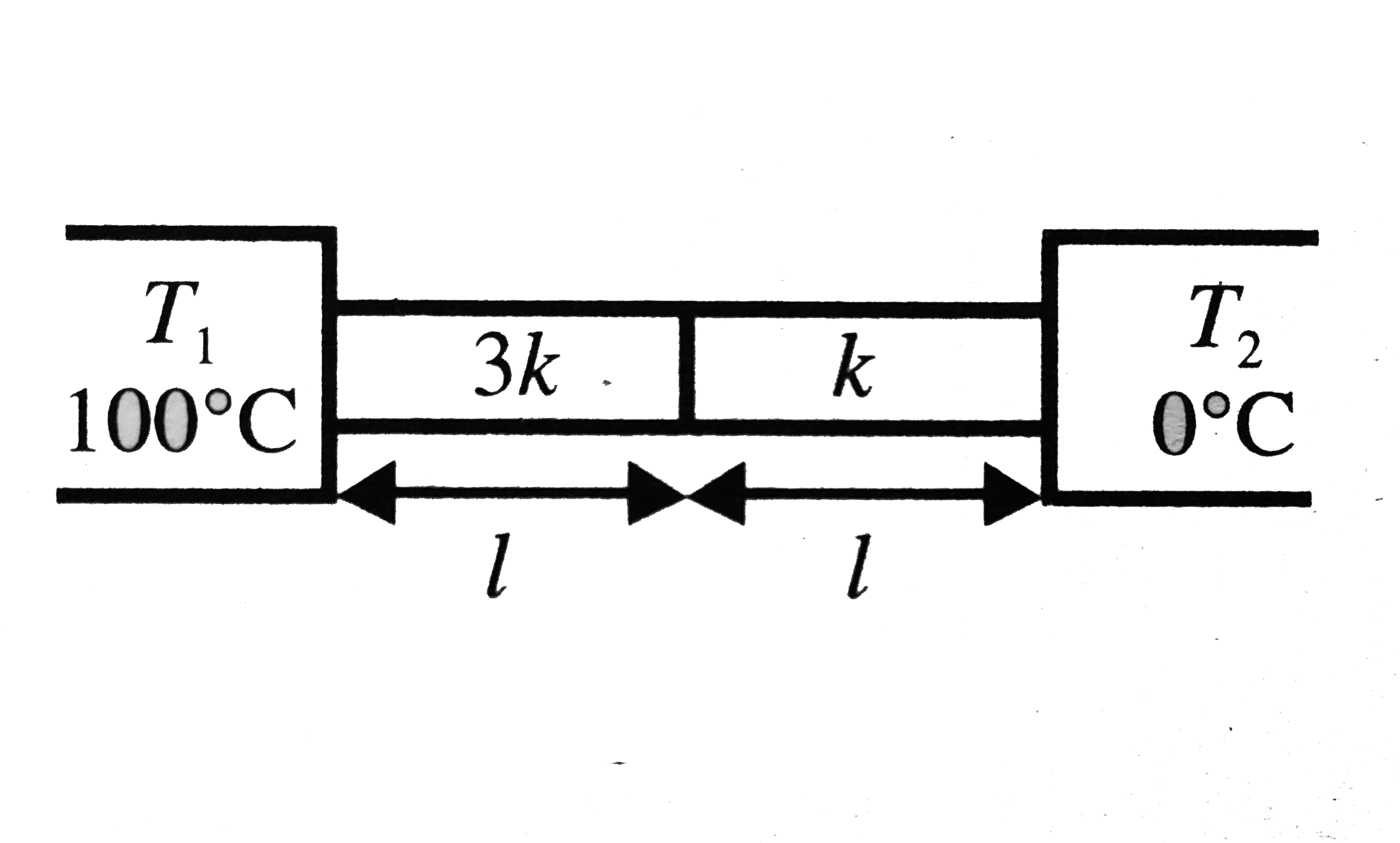
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.View Solution-
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.View Solution Two rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.
View SolutionThe lleft end of a copper rod (≤n>h=20cm.Areaofcrosssection=0.02cm2 is maintained at 20∘C and the right end is maintained at 80∘C . Neglecting any lkkoss of heat through radiation, find (a) the temperature at a point 11cm from the left end and (b) the heat current through the rod. thermal conductivity of copper =385Wm=−1^(@)C^(-1) .
View SolutionOne end of a metal rod of length 1.0 m and area of cross section 100cm2 is maintained at . 100∘C. If the other end of the rod is maintained at 0∘C , the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod =100W/m−K)
View Solution