Show that the radius of the orbit in hydrogen atom varies as , where it is the principal quantum number of the atom.
We know that when an electron revolves in a stable orbit, the centripetal force is provided by electrostatic force of attraction acting on it due to a proton present in the nucleus.
and from Bohr.s quantum condition , we have .
Squaring (ii) and then equating it with (i) , we get .
In stable orbit of hydrogen atom n = 1 and then radius of 1st orbit is called Bohr.s radius . Obviously
Topper's Solved these Questions
- ATOMSBOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - LONG ANSWER QUESTIONS - I
18 Videos
- ATOMSBOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - LONG ANSWER QUESTIONS - II
4 Videos
- ATOMSBOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - VERY SHORT ANSWER QUESTIONS.
20 Videos
- ALTERNATING CURRENT BOOK - U-LIKE SERIESCHAPTER - ALTERNATING CURRENT EXERCISE - SELF ASSESSMENT TEST (SECTION -C)
2 Videos
- CBSE EXAMINATION PAPER 2020 BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 EXERCISE - SECTION D
12 Videos
Similar Questions
Show that the radius of the orbit in hydrogen atom varies as n2, where n is the principal quantum number of the atom.
View Solution(a) Define the distance of closest approach. A α -particle of kinetic energy K is bombarded on a thin gld foil. The distance of the closest approach is ra. What will be the distance of closest approach for an α-particle of double the kinetic energy ?
(b) Show that the radius of the orbit of an electron in hydrogen atoms varies as n2, where n is the principal quantum number of the atom.
View Solution
Knowledge Check
The energy of an excited hydrogen atom is -3.4eV. The principal quantum number of the orbit is
A1B2C3D4The radius of the hydrogen atom in its ground state is 5.3×10−11 m. The principal quantum number of the final state of the atom is
A2B3C4D16Which of the following curves may represent the speed of the electron in a hydrogen atom as a function of the principal quantum number n ?
A B
B C
C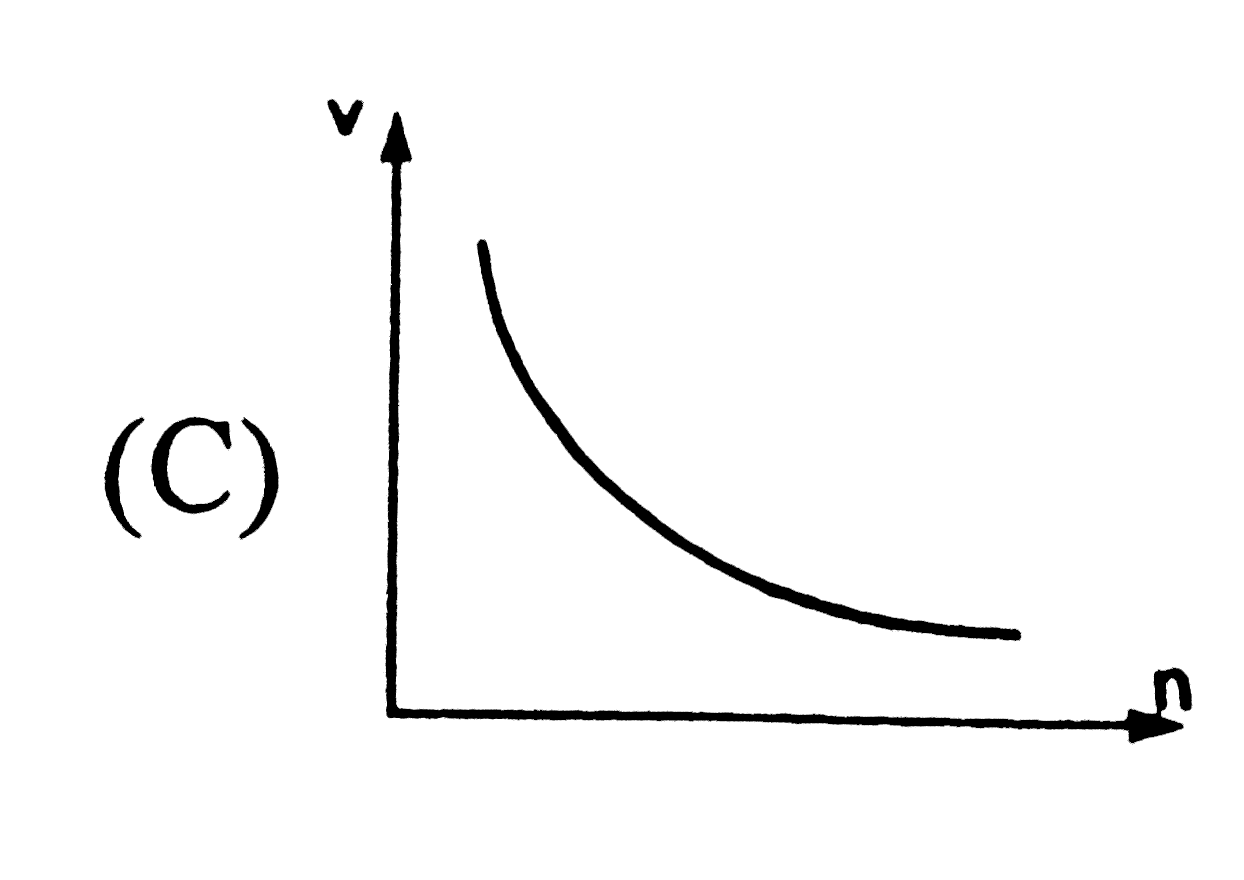 D
D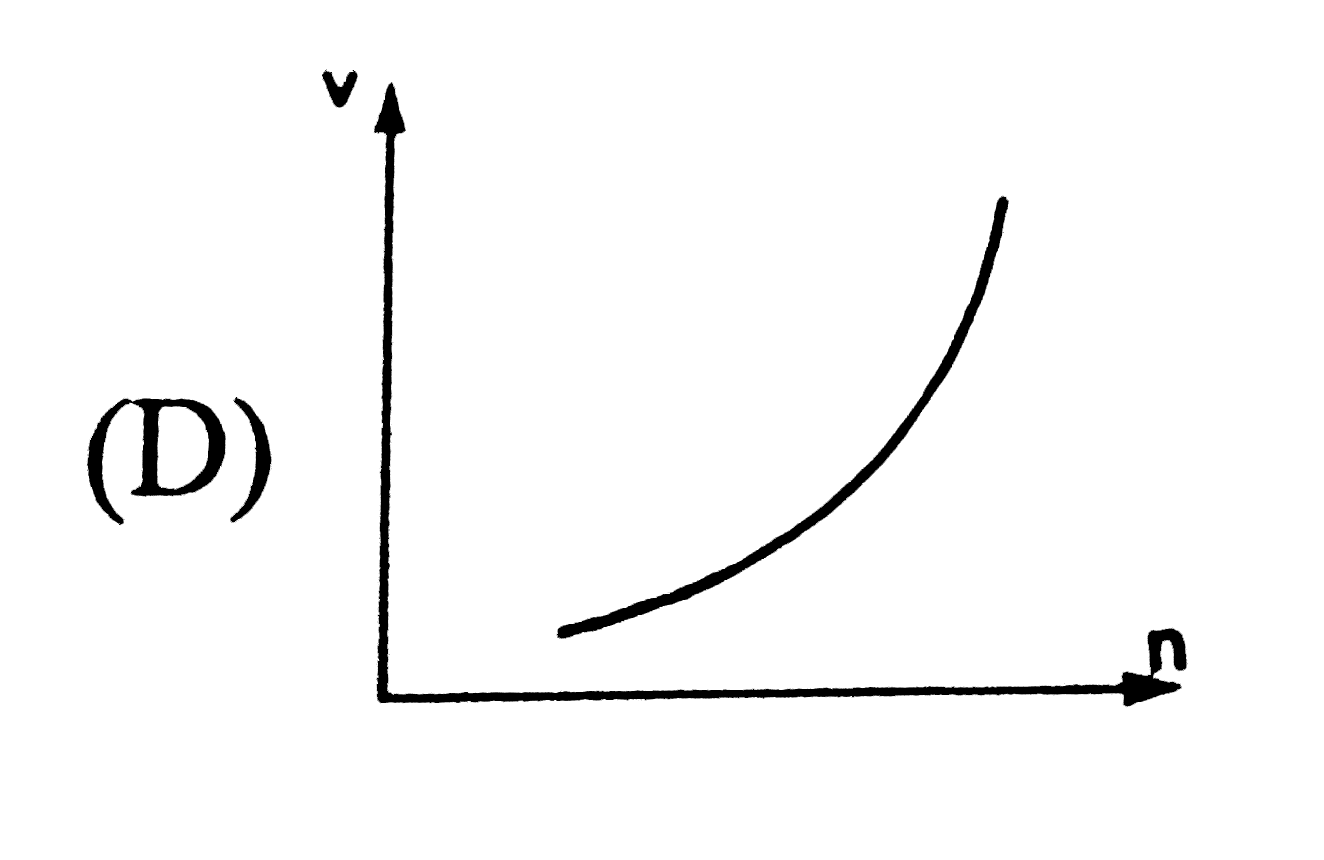
The principal quantum number determines ……….of the atom
View SolutionThe principal quantum number determines ……….of the atom
View SolutionThe radii of Bohr's orbit are directly proportional to
View SolutionUsing the expression for the radius of orbit for Hydrogen atom , show that the linear speed varies inversely to principal quantum number n the angular speed varies inversely to the cube of principal quantum number n.
View SolutionPrincipal quantum number of an atom represents :
View Solution
