As observed in the laboratory system , a 6 MeV proton is incident on a stationary 12 C target. The velocity of centre of mass of the system is (Take mass of proton to be 1 amu)
The correct Answer is:A
To find the velocity of the center of mass (V_com) of a system consisting of a proton and a stationary carbon-12 target, we can follow these steps:
Step 1: Identify the masses and kinetic energy
- Mass of the proton (m₁) = 1 amu
- Mass of the carbon-12 nucleus (m₂) = 12 amu
- Kinetic energy (KE) of the proton = 6 MeV
Step 2: Convert kinetic energy from MeV to Joules
1 MeV = 1.6×10−13 Joules. Therefore,
KE=6MeV=6×1.6×10−13J=9.6×10−13J
Step 3: Relate kinetic energy to momentum
The relationship between kinetic energy (KE) and momentum (p) is given by:
KE=p22m
From this, we can express momentum as:
p=√2m⋅KE
Step 4: Calculate the momentum of the proton
Using the mass of the proton (m₁ = 1 amu), we can calculate the momentum:
p=√2⋅1amu⋅9.6×10−13J
Step 5: Substitute the values and simplify
Convert 1 amu to kg:
1amu=1.67×10−27kg
Thus, the momentum becomes:
p=√2⋅(1.67×10−27kg)⋅(9.6×10−13J)
Step 6: Calculate the center of mass velocity
The velocity of the center of mass (V_com) is given by:
Vcom=pm1+m2
Substituting the values:
Vcom=p1amu+12amu=p13amu=p13⋅1.67×10−27kg
Step 7: Final calculation
Now we can substitute the value of momentum (p) into the equation for V_com and calculate it:
Vcom=√2⋅(1.67×10−27)⋅(9.6×10−13)13⋅1.67×10−27
Step 8: Solve for V_com
After performing the calculations, we find:
Vcom≈2.6×106m/s
Conclusion
The velocity of the center of mass of the system is approximately 2.6×106m/s.
---
- Mass of the proton (m₁) = 1 amu
- Mass of the carbon-12 nucleus (m₂) = 12 amu
- Kinetic energy (KE) of the proton = 6 MeV
1 MeV = 1.6×10−13 Joules. Therefore,
KE=6MeV=6×1.6×10−13J=9.6×10−13J
The relationship between kinetic energy (KE) and momentum (p) is given by:
KE=p22m
From this, we can express momentum as:
p=√2m⋅KE
Using the mass of the proton (m₁ = 1 amu), we can calculate the momentum:
p=√2⋅1amu⋅9.6×10−13J
Convert 1 amu to kg:
1amu=1.67×10−27kg
Thus, the momentum becomes:
p=√2⋅(1.67×10−27kg)⋅(9.6×10−13J)
The velocity of the center of mass (V_com) is given by:
Vcom=pm1+m2
Substituting the values:
Vcom=p1amu+12amu=p13amu=p13⋅1.67×10−27kg
Now we can substitute the value of momentum (p) into the equation for V_com and calculate it:
Vcom=√2⋅(1.67×10−27)⋅(9.6×10−13)13⋅1.67×10−27
After performing the calculations, we find:
Vcom≈2.6×106m/s
The velocity of the center of mass of the system is approximately 2.6×106m/s.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The velocity (in m/s) of centre of mass of the system as shown in the figure is :
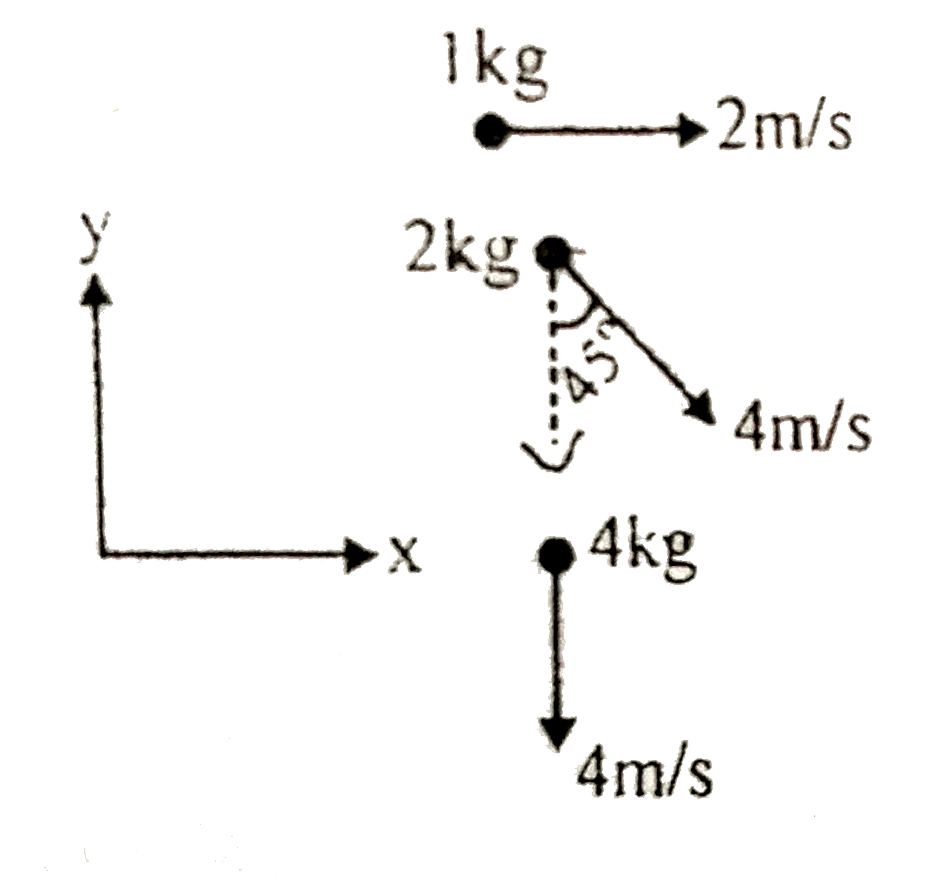 A2[1+4√2]ˆi+8[1√2+2]ˆj7B2[1+4√2]ˆi+8[1√2−2]ˆj7C2[1+4√2]ˆi−8[1√2+2]ˆj7D8[1√2−2]ˆi+2[1+4√2ˆj]7
A2[1+4√2]ˆi+8[1√2+2]ˆj7B2[1+4√2]ˆi+8[1√2−2]ˆj7C2[1+4√2]ˆi−8[1√2+2]ˆj7D8[1√2−2]ˆi+2[1+4√2ˆj]7The velocity of centre of mass of the system remains constant, if the total external force acting on the system is.
AminimumBmaximumCunityDzeroA proton with energy of 2 MeV enters a region of a uniform magnetic field of 2.5 T normally. The magnetic force on the proton is (Take mass of proton to be
A3×10−12NB3×10−8NC8×10−12ND3×10−10N
Revision|Motion Of Centre Of Mass|Velocity Of Centre Of Mass|Two Particle System|OMR
View SolutionCentre OF Mass OF Continuous System - 1
View Solution1 amu = 112 the mass of one C-12 atom .
View SolutionStatement-1 : The centre of mass of a system of n particles is the weighted average of the position vector of the n particles making up the system
. Statement-2 : The position of the centre of mass of a system is independent of coordinate system
View SolutionTwo bodies of masses 1 kg and 2 kg, separated by 6 m are rotating about the centre of mass of the system. The moment of inertia of the system is
View Solution
