If net flux through a Caussian surface is zero, then find whether the following statements are correct or not.
The number of field lines entering the surface equals to the number of field lines leaving the surface.
To determine whether the statements are correct when the net electric flux through a Gaussian surface is zero, we can follow these steps:
Step 1: Understand the concept of electric flux
Electric flux (Φ) through a surface is defined by the equation:
Φ=Qenclosedϵ0
where Qenclosed is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
Step 2: Analyze the condition of zero net flux
If the net flux through the Gaussian surface is zero, we can write:
Φnet=0
This implies:
Qenclosedϵ0=0
From this equation, we can conclude that:
Qenclosed=0
This means that the total charge inside the Gaussian surface is zero.
Step 3: Relate charge to electric field lines
Electric field lines represent the presence of electric charge. If the total charge enclosed by the Gaussian surface is zero, it implies that the number of electric field lines entering the surface must equal the number of electric field lines leaving the surface. This is because any field lines that enter the surface must exit, maintaining the balance due to the absence of any net charge.
Step 4: Conclusion
Thus, we can conclude that the statement "The number of field lines entering the surface equals the number of field lines leaving the surface" is correct when the net flux through a Gaussian surface is zero.
Final Answer
The statement is correct.
---
Electric flux (Φ) through a surface is defined by the equation:
Φ=Qenclosedϵ0
where Qenclosed is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
If the net flux through the Gaussian surface is zero, we can write:
Φnet=0
This implies:
Qenclosedϵ0=0
From this equation, we can conclude that:
Qenclosed=0
This means that the total charge inside the Gaussian surface is zero.
Electric field lines represent the presence of electric charge. If the total charge enclosed by the Gaussian surface is zero, it implies that the number of electric field lines entering the surface must equal the number of electric field lines leaving the surface. This is because any field lines that enter the surface must exit, maintaining the balance due to the absence of any net charge.
Thus, we can conclude that the statement "The number of field lines entering the surface equals the number of field lines leaving the surface" is correct when the net flux through a Gaussian surface is zero.
The statement is correct.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) FILL IN THE BLANKS4videos
ELECTROSTANTICS
- BOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL - II & III15videos
ELECTROSTANTICS
- BOOK - FIITJEECHAPTER - ELECTROSTANTICSEXERCISE - EXERCISE10videos
ELECTROSTANTICS
- BOOK - FIITJEECHAPTER - ELECTROMAGNETIC WAVE & WAVE OPTICSEXERCISE - ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)21videos
ELECTROMAGNETIC WAVE & WAVE OPTICS
- BOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example14videos
ELECTROSTATICS
Similar Questions
If net flux through a Caussian surface is zero, then find whether the following statements are correct or not.
There are no changes inside the surface.View SolutionIf net flux through a Gaussian surface is zero, then find whether the following statements are correct or not.
The net charge inside the surface is zero.View Solution
Knowledge Check
- Question 1 - Select One
If the net electric flux through a closed surface is zero, then we can infer
Ano net charge is enclosed by the surfaceBuniform electric field exists within the surfaceCelectric potential varies from point to point inside the surfaceDcharge is present inside the surface - Question 2 - Select One
When field lines are leaving a surface the flux will be taken as
ApositiveBnegativeCdepens on the surfaceDneither positive nor negative - Question 3 - Select One or More
An imaginary closed surface P is constructed around a neutral conducting wire connected to a battery and a switch as shown in figure. As the switch is closed, the free electrons in the wire start moving along the wire. In any time interval, the number of electrons entering the closed surface P is equal to the number of electrons leaving it. On closing the switch, the flux of the electric field through the closed surface :
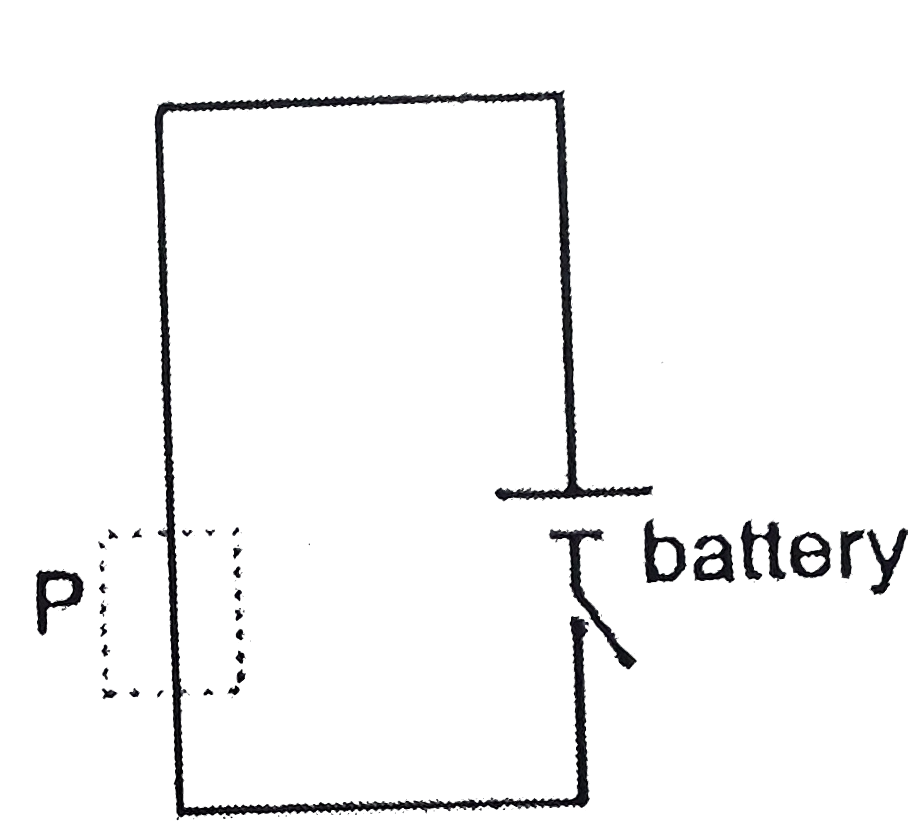 Aremains unchangedBremains zeroCis increasedDis decreased
Aremains unchangedBremains zeroCis increasedDis decreased
Find out flux through given gaussian surface.
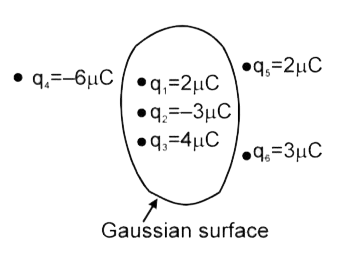 View Solution
View SolutionIf electric flux passing through a close surface is zero then :-
View SolutionFind out flux through the given Gaussian surface.
 View Solution
View SolutionFind flux through the hemispherical surface
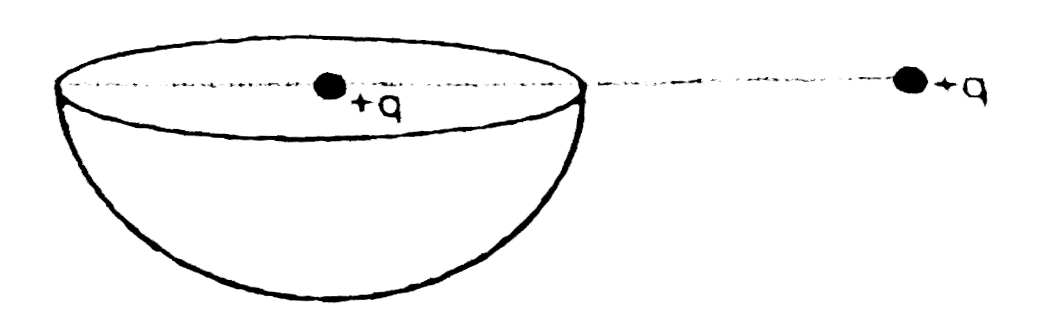 View Solution
View SolutionFind flux through the hemispherical surface
 View Solution
View Solution

