The line joining the midpoints of any two sides of a triangle is parallel to 3rd side and equal to half of it
To solve the problem based on the statement "The line joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it," we can follow these steps:
1. Identify the Triangle and Midpoints:
Let triangle ABC be given, where points D and E are the midpoints of sides AB and AC, respectively.
Hint: Remember that the midpoints are the points that divide the sides into two equal segments.
2. Draw the Line Segment DE:
Connect points D and E to form line segment DE.
Hint: Visualize how connecting the midpoints creates a new line segment within the triangle.
3. Apply the Midpoint Theorem:
According to the Midpoint Theorem, the line segment DE is parallel to side BC and its length is half of the length of BC.
Hint: Recall that the Midpoint Theorem states that the segment connecting the midpoints of two sides of a triangle is parallel to the third side.
4. Establish the Relationship:
Since DE is parallel to BC, we can conclude that DE = 1/2 * BC.
Hint: Think about how parallel lines create corresponding angles that are equal, which helps in establishing proportional relationships.
5. Use the Properties of Triangles:
Since DE is parallel to BC, triangles ADE and ABC are similar by the AA (Angle-Angle) criterion.
Hint: Similar triangles have corresponding sides that are proportional.
6. Conclude the Proof:
Therefore, we have shown that the line joining the midpoints of any two sides of triangle ABC is parallel to the third side and is equal to half of it.
Hint: Summarize your findings by restating the theorem and the conditions under which it holds true.
Final Conclusion:
The line segment joining the midpoints of any two sides of a triangle is indeed parallel to the third side and is equal to half of that side, as demonstrated through the application of the Midpoint Theorem and properties of similar triangles.
Let triangle ABC be given, where points D and E are the midpoints of sides AB and AC, respectively.
Connect points D and E to form line segment DE.
According to the Midpoint Theorem, the line segment DE is parallel to side BC and its length is half of the length of BC.
Since DE is parallel to BC, we can conclude that DE = 1/2 * BC.
Since DE is parallel to BC, triangles ADE and ABC are similar by the AA (Angle-Angle) criterion.
Therefore, we have shown that the line joining the midpoints of any two sides of triangle ABC is parallel to the third side and is equal to half of it.
The line segment joining the midpoints of any two sides of a triangle is indeed parallel to the third side and is equal to half of that side, as demonstrated through the application of the Midpoint Theorem and properties of similar triangles.
Similar Questions
Knowledge Check
Assertion : ABCD and PQRC are rectangles and Q is a midpoint of AC. Then DP = PC.
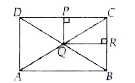
Reason : The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.
In the given figure, the side AC of ΔABC is produced to E such that CE = FAC. If D is the midpoint of BC and ED produced meets AB at F and CP, DQ are drawn parallel to BA, then FD=
 A12FEB13EFC2FEDFE
A12FEB13EFC2FEDFE
Prove that the line segment joining the mid points of two side of a triangle is parallel to the third side and equal to half of it.
View SolutionUsing Theorem 6.2, prove that the line joining the mid-point of any two sides of a triangle is parallel to the third side. (Recall that you have done it in class IX).
View SolutionThe line segment joining the mid-points of any two sides of a triangle is parallel to the third side of a triangle.
View SolutionThe line joining the mid-points of two sides of a triangle is parallel to the third side.
View Solutionprove that the line segment joining the mid-points of two sides of a triangle is parallel to the third side.
View SolutionProve that the line joining the mid-points of the two sides of a triangle is parallel to the third side.
View Solution
