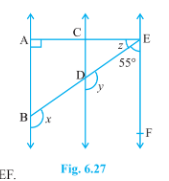
In Fig. 6.30, if AB∣∣CD, EF⊥CD and ∠GED=126∘, find ∠AGE,∠GEF and ∠FGE.
∠AGE=∠GED=126∘
(Alternate angles)
∠GED=∠GEF+∠FED126∘=∠GEF+90∘∠GEF=126∘−90∘=36∘
∠CEG+∠GED=180∘
(Supplementary angles)
∠CEG+126∘=180∘
∠CEG=180∘−126∘=54∘
∠FGE=∠CEG=54∘
(Alternate angles )
Topper's Solved these Questions
- LINES AND ANGLESBOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES
8 Videos
- LINES AND ANGLESBOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.1
6 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NCERTCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - EXERCISE 4.4
2 Videos
- NCERT THEOREMSBOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.12
1 Videos
Similar Questions
Knowledge Check
Ab Bc Cd De Ef Fg G?
AiBHCIDhIn the figure , AB∣∣CD and PQ,QR intersect AB and CD both at E, F G and H respectively. Given that ∠PEB=80∘,∠QHD=120∘ and ∠PQR=x, then find the value of x .
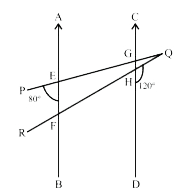 A40∘B20∘C100∘D30∘
A40∘B20∘C100∘D30∘
In Fig. 6.13, lines AB and CD intersect at O. If ∠AOC +∠BOE=70∘and ∠BOD=40∘, find ∠BOE and reflex ∠COE.
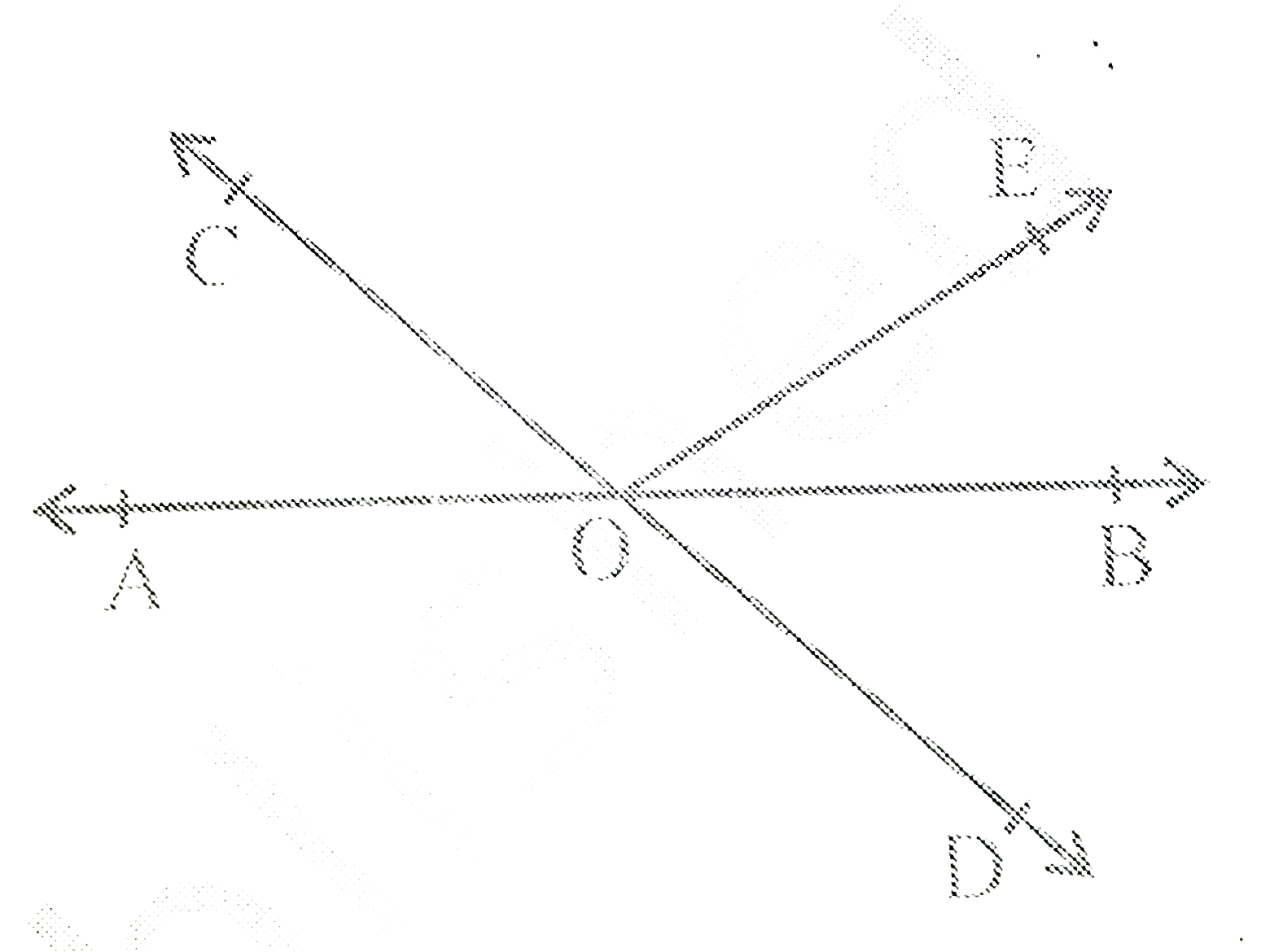
View SolutionIn Fig.102, ABCDEF, ∠ABG=1100,∠GCD=1000 and ∠BGC=x0. the value of x is (a) 35 (b) 50 (c) 30 (d) 40
View SolutionIn Fig. 4.102 (i) and (ii) , if CD and GH (D and H lie on AB and FE ) are respectively bisectors of ∠ACB and ∠EGF and ABC~FEG , prove that (FIGURE) DCA~HGF (ii) CDGH=ACFG (iii) DCB~HGE
View SolutionIn the six cornered figure, (fig.20), AC,AD and AE are joined. Find ∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠EFA.
View SolutionIn Fig. 4.128, DEFG is a square and ∠BAC=90o . Prove that AGFDBG (ii) AGFEFC (FIGURE) (iii) DBGEFC (iv) DE2=BD×EC
View SolutionIn Fig. 4.103, CD and GH are respectively the medians of ABC and EFG . If ABC~FEG , prove that (FIGURE) ADC~FHG (ii) CDGH=ABFE (iii) CDB~GHE
View Solution