In Fig. 6.16, if x+y=w+z, then prove that AOB is a line.
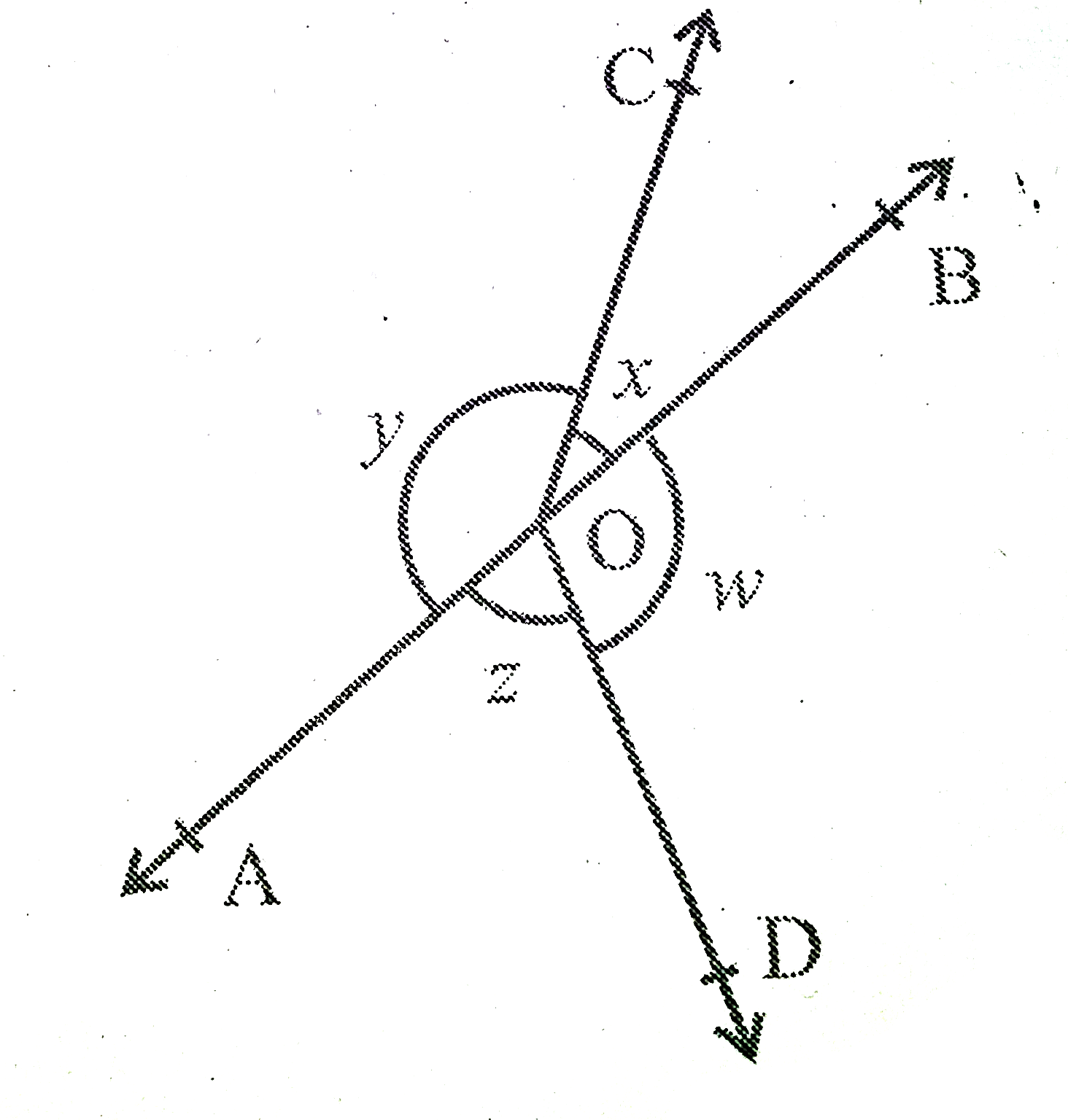
∠BOC+∠COA+∠AOD+∠DOB=360∘
x+y+z+w=360∘
(x+y)+(w+z)=360∘
(x+y)=(w+z)=180∘non common arms of angles forms a line
putting this value in equation (1)
2(x+y)=360∘
(x+y)=180∘
so, AOB is a line.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - EXERCISE 6.26videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES8videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES8videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - EXERCISE 4.42videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.121videos
NCERT THEOREMS
Similar Questions
In Figure, if x+y=w+z, then prove that AOB is a line Fig.
 View Solution
View SolutionIn Fig. 6.16, if x+y=w+z, then prove that AOB is a line.
 View Solution
View SolutionIn the given figure, if x+y=z+w then prove that AOB is a line.
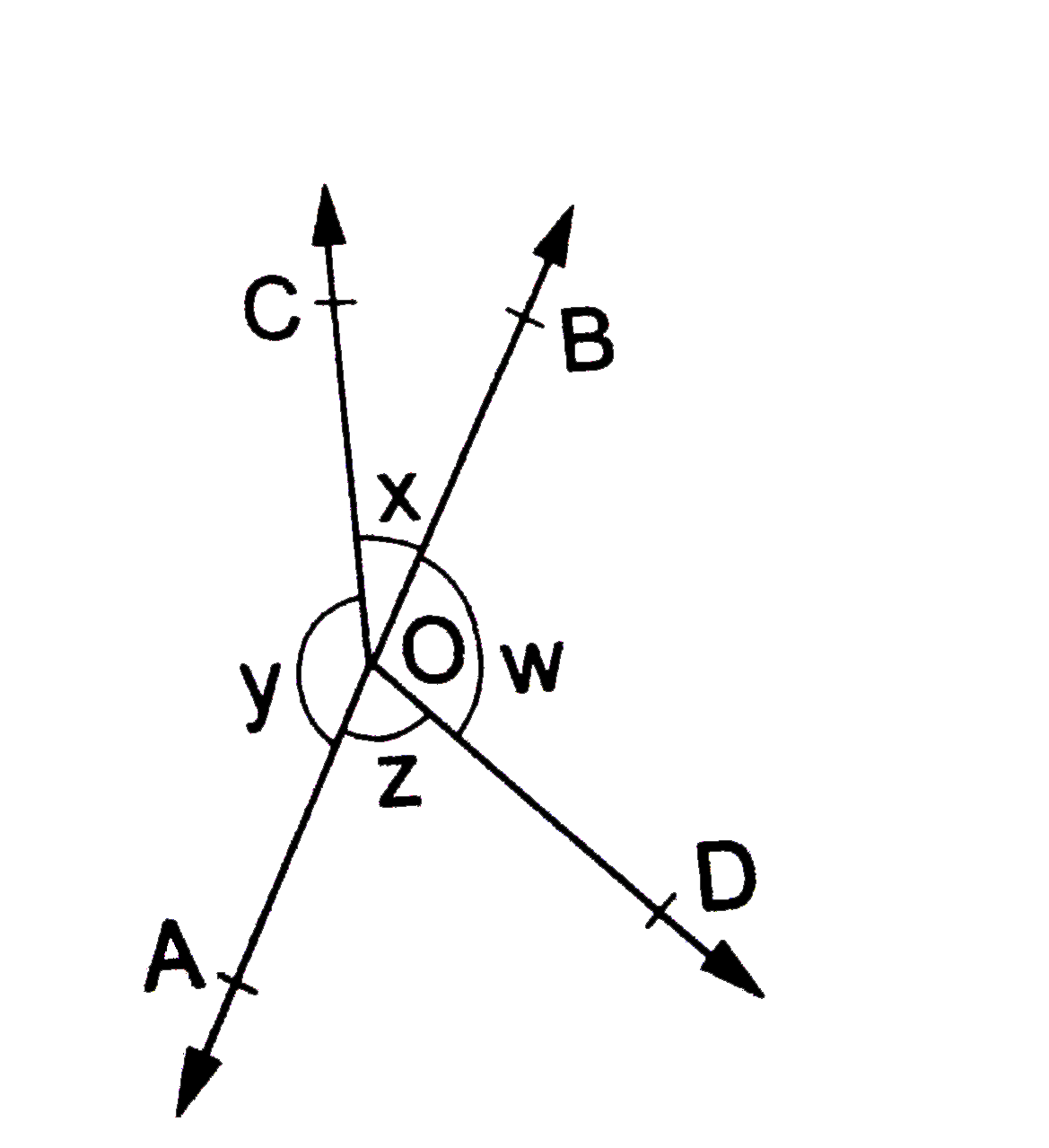 View Solution
View SolutionIn Fig. 4.97, if ∠A=∠C , then prove that AOB~COD . (FIGURE)
View SolutionA line perpendicular to the axis of the parabola y2=16x intersects the parabola in two points A and B . If AB = 32 , show that ∠AOB is a right angle . Also , find the area of ΔAOB .
View SolutionIn Fig. 6.40, find the values of x, y and z.
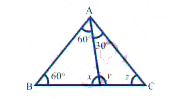 View Solution
View SolutionIn Fig. 6.46, if y is five times x, find the value of z.
 View Solution
View SolutionIf ω≠1 is a cube root of unity and x+y+z≠0, then prove that ∣∣∣x1+ωyω+ω2zω2+1yω+ω2zω2+1x1+ωzzω2+1x1+ωyω+ω2∣∣∣=0 if x=y=z
View SolutionIf the 4th, 10th and 16th terms of a GP are x, y, z respectively, prove that x, y, z are in GP.
View SolutionIf ω is non-real cube roots of unity, then prove that ∣∣∣x+yω+zω2xw+z+yω2∣∣∣=1
View Solution

