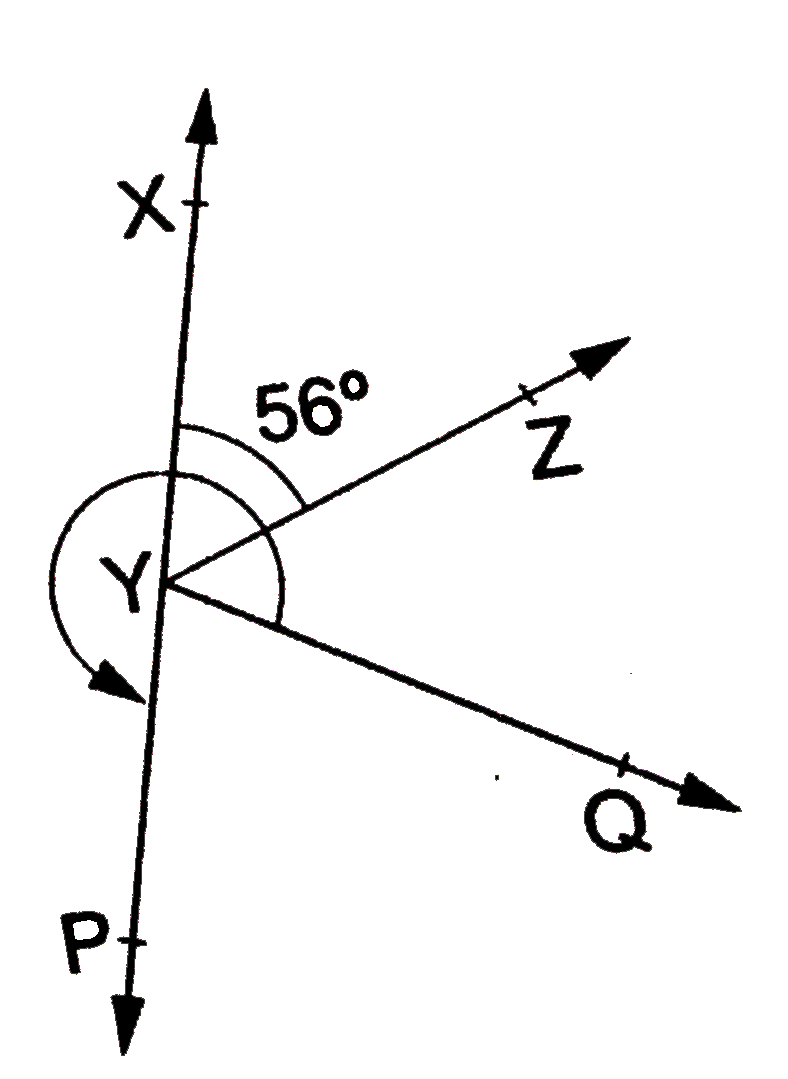
It is given that and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects , find and reflex .
To solve the problem step by step, we will first draw the necessary figure based on the given information, and then we will calculate the required angles.
Step 1: Draw the Figure
1. Draw a line segment XY.
2. Extend the line segment XY to point P.
3. Mark point Z such that angle ∠XYZ = 64°.
4. Draw ray YQ such that it bisects angle ∠ZYP.
Step 2: Identify Angles
- Let:
- ∠XYZ = 64° (given)
- ∠ZYP = angle formed by rays ZY and YP.
- Let ∠QYP be the angle formed by rays YQ and YP.
- Let ∠XYQ be the angle formed by rays XY and YQ.
Step 3: Use the Angle Bisector Theorem
Since ray YQ bisects angle ∠ZYP:
- We can denote:
- ∠QYP = ∠ZYW (let's call this angle 1)
- ∠XYQ = ∠ZYP (let's call this angle 2)
Step 4: Express the Angles in Terms of Each Other
From the figure, we know that:
- ∠ZYP = ∠QYP + ∠XYQ
- Since ∠QYP is equal to ∠ZYW (angle 1), we can write:
- ∠ZYP = 2 * ∠QYP + 64° (because ∠ZYP = ∠QYP + ∠XYQ)
Step 5: Set Up the Equation
Using the fact that the sum of angles on a straight line is 180°:
- ∠QYP + ∠XYQ + ∠XYZ = 180°
- Substitute the known values:
- ∠QYP + ∠XYQ + 64° = 180°
Step 6: Solve for ∠QYP
Let ∠QYP = x (angle 1):
- Then ∠XYQ = 64° + x (angle 2)
- Substitute into the equation:
- x + (64 + x) + 64 = 180
- 2x + 128 = 180
- 2x = 180 - 128
- 2x = 52
- x = 26
Thus, ∠QYP = 26°.
Step 7: Find ∠XYQ
Now we can find ∠XYQ:
- ∠XYQ = 64° + ∠QYP
- ∠XYQ = 64° + 26° = 90°
Step 8: Find the Reflex Angle ∠QYP
To find the reflex angle ∠QYP:
- Reflex ∠QYP = 360° - ∠QYP
- Reflex ∠QYP = 360° - 26° = 334°
Final Answers
- ∠XYQ = 90°
- Reflex ∠QYP = 334°
1. Draw a line segment XY.
2. Extend the line segment XY to point P.
3. Mark point Z such that angle ∠XYZ = 64°.
4. Draw ray YQ such that it bisects angle ∠ZYP.
- Let:
- ∠XYZ = 64° (given)
- ∠ZYP = angle formed by rays ZY and YP.
- Let ∠QYP be the angle formed by rays YQ and YP.
- Let ∠XYQ be the angle formed by rays XY and YQ.
Since ray YQ bisects angle ∠ZYP:
- We can denote:
- ∠QYP = ∠ZYW (let's call this angle 1)
- ∠XYQ = ∠ZYP (let's call this angle 2)
From the figure, we know that:
- ∠ZYP = ∠QYP + ∠XYQ
- Since ∠QYP is equal to ∠ZYW (angle 1), we can write:
- ∠ZYP = 2 * ∠QYP + 64° (because ∠ZYP = ∠QYP + ∠XYQ)
Using the fact that the sum of angles on a straight line is 180°:
- ∠QYP + ∠XYQ + ∠XYZ = 180°
- Substitute the known values:
- ∠QYP + ∠XYQ + 64° = 180°
Let ∠QYP = x (angle 1):
- Then ∠XYQ = 64° + x (angle 2)
- Substitute into the equation:
- x + (64 + x) + 64 = 180
- 2x + 128 = 180
- 2x = 180 - 128
- 2x = 52
- x = 26
Now we can find ∠XYQ:
- ∠XYQ = 64° + ∠QYP
- ∠XYQ = 64° + 26° = 90°
To find the reflex angle ∠QYP:
- Reflex ∠QYP = 360° - ∠QYP
- Reflex ∠QYP = 360° - 26° = 334°
- ∠XYQ = 90°
- Reflex ∠QYP = 334°
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - EXERCISE 6.26videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES8videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES8videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - EXERCISE 4.42videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.121videos
NCERT THEOREMS
Similar Questions
Knowledge Check
- Question 1 - Select One
If AM and GM of x and y are in the ratio of p:q, then x:y is
Ap−√p2+q2:√p2+q2Bp+√p2−q2:p−√p2−q2Cp:qDp+√p2+q2:p−√p2+q2 - Question 2 - Select One
A, Q, Y, Z are different persons. Z is the father of Q . A is the daughter of y and y is the son of Z. If P is the son of Y and B is the brother of P, then
Aa. B and Y are brotherBb. A is the sister of BCc. Z is the uncle of BDd. Q and Y are brothers - Question 3 - Select One
P @ Q means P is greater than Q.
P @–– Q means P is either greater than or equal to Q.
P = Q means P is equal to Q.
P © Q means P is smaller than Q.
P ©– Q means P is either smaller than or equal to Q.
Statements: X@Y,Z©–R,Y=Z
Conclusions: I. X @ R II. Y = RAIf only I is trueBif only conclusion II is trueCif either conclusion I or II is trueDif either I nor II is true
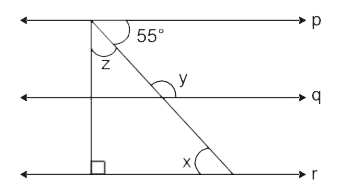
If p||q||r, find x,y,z from given figure .
 View Solution
View Solution
In the figure given above, p and q are parallel lines. What are the values of the angles x, y and z?View SolutionGiven that logxy,logzx,logyz are in GP, xyz=64 and x3,y3,z3 are in A.P.
Which one of the following is correct ?
xy,yz and zx areView SolutionGiven that logxy,logzx,logyz are in GP, xyz=64 and x3,y3,z3 are in A.P.
Which one of the following is correct ?
x,y and z areView SolutionGiven that logxy,logzx,logyz are in GP, xyz=64 and x3,y3,z3 are in AP.
Q. Which one of the following is correct ? x,y and z areView Solution