Consider the decay scheme- A→B→C with λA<λB.After transient equilibrium is established between A and B , show that the interval of timeΔt, such that activity of A at t−Δt.is equal toa ctivity of B at 't' is given by Δt=ιAIn(λBλB−A) and that this approaches TB,as(TBTA) rarr 0
Let N1 be the amount of parent atom of A at any instant t−Δt.Therefore, N1=N01e−λA(t−Δt)…..(1),Where N01 is the number of parent atom of A at t=0.The number of daughter atoms at anytime t is given by N2=λAN01λB−λA[e−λAt−e−λBt].......(2),For transient atom λA<λB, hence e−λB , t term can be neglected in (2) ∴N2−λAN01λB−λAe−λAt........(3)Given that activity of A at (t−Δt)=activityofBatt.implieslambda _(A) N_(1)^(0) e^(-lambda _(A)(t-Delta t))=lambda_(B) (lambda_(A) N_(1)^(0) )/(lambda_(B)-lambda _(A))e^(-lambda_(A)t),impliese^(-lambda _(A) Delta t)=(lambda_(B))/(lambda _(B)-lambda_(A))impliesDelta t=(1)/(lambda_(A))In [(lambda_(B))/(lambda_(B)-lambda_(A))].TheavergaelifeofAiota =(1)/(lambda_(A))andtˆofBisiota =(1)/(lambda_(B)) ,thereforeDelta t =iota _(A)In[(1)/((1-lambda_(B))/(lambda_(A)))] implies Delta t cong iota _(A).(iota_(B))/(iota_(A))asiota _(B)/iota _(A) rArr 0(given)impliesDelta t= iota _(B)
Topper's Solved these Questions
Similar Questions
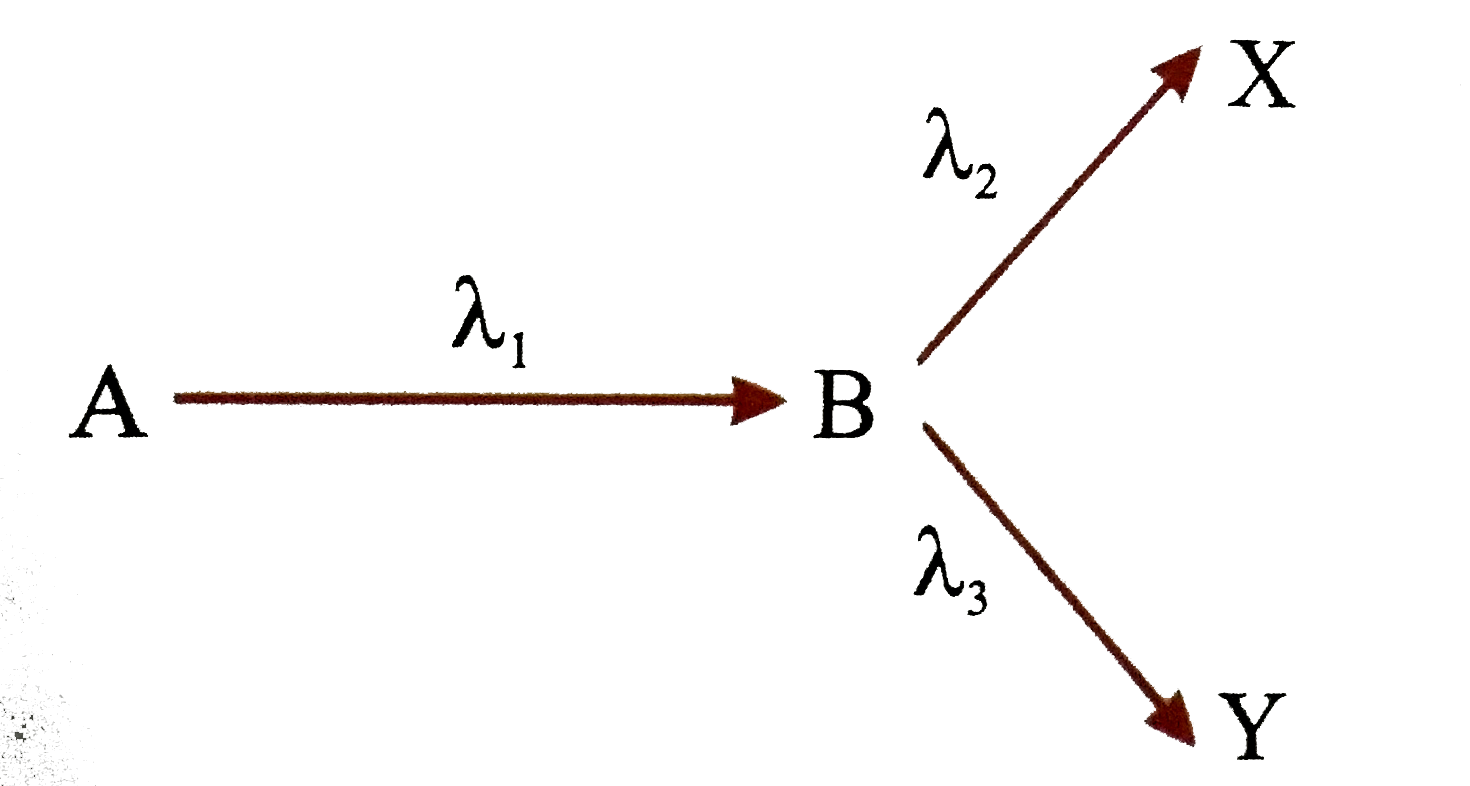
Consider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
The net rate of accumulation of B at any instant isView SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
The net rate of accumulation of B at any instant isView Solution
Knowledge Check
- Question 1 - Select One
Consider a nuclear decay process A→B→C(stab≤)
At a certain time, the activity of nuclei A is 'x' and the nett rate of increase of number of nuclei B is 'y' The activity of nuclei B at this instant is :AyBx−yCy−xDx - Question 2 - Select One
Consider this reaction: A+B→C+D+ energy
Athis reaction is exergonicBan enzyme could still speed the reactionCA and B are reactants, C and D are productsDall of the above are correct - Question 3 - Select One
Consider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
At t=∞, which of following is incorrect ?AN2=0BN3=N0λ2λ2+λ3CN4=2N0λ3λ2+λ3DN1+N2+N3+N4=2N0
The average (mean) life of a radio nuclide which decays by parallel path is
Aλ1−−→B : λ1=1.8×10−2sec−1
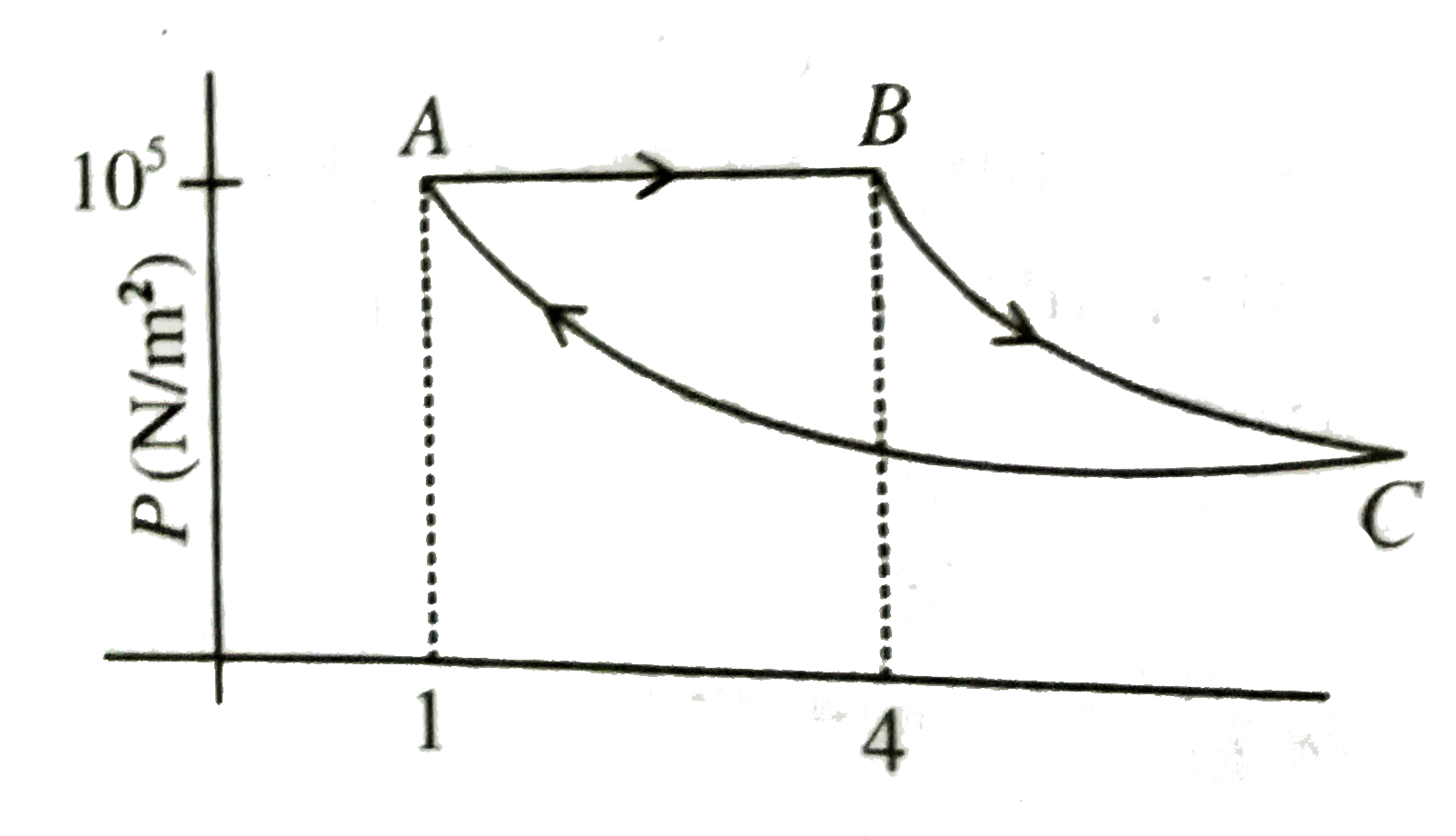
2Aλ2−−→B , λ2=10−3sec−1View SolutionA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal. Find pressure at C
.View SolutionThe average (mean) life of a radio nuclide which decays by parallel path is
Aλ1−−→B : λ1=1.8×10−2sec−1
2Aλ2−−→B , λ2=10−3sec−1View SolutionA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal.
Find pressure at C.View SolutionA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal.
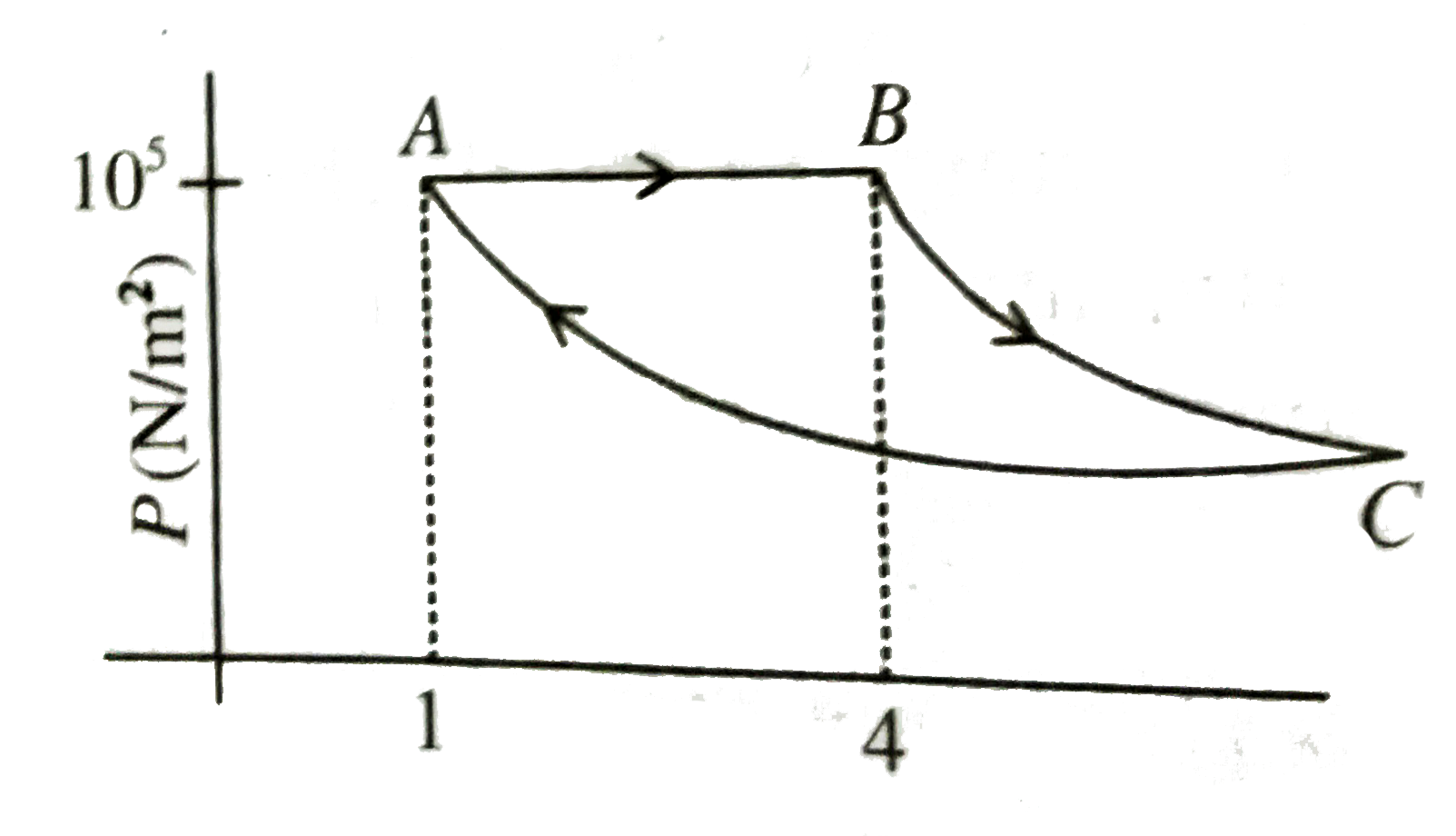Find volume at C. View Solution