A child weighing 25 kg slides down a rope hanging from a branch of a tall tree. If the force of friction acting against him is 200 N, the acceleration of child is (g=10m/s2)
22.5m/s2
8m/s2
5m/s2
2m/s2
To solve the problem of the child sliding down the rope, we can follow these steps:
Step 1: Identify the forces acting on the child
The forces acting on the child are:
1. The gravitational force (weight) acting downwards, which can be calculated using the formula:
Fgravity=m⋅g
where m=25kg and g=10m/s2.
2. The force of friction acting upwards, which is given as Ffriction=200N.
Step 2: Calculate the gravitational force
Substituting the values into the formula:
Fgravity=25kg⋅10m/s2=250N
Step 3: Determine the net force acting on the child
The net force (Fnet) acting on the child can be calculated by subtracting the force of friction from the gravitational force:
Fnet=Fgravity−Ffriction=250N−200N=50N
Step 4: Apply Newton's second law
According to Newton's second law, the net force is also equal to the mass of the child multiplied by its acceleration:
Fnet=m⋅a
Substituting the known values:
50N=25kg⋅a
Step 5: Solve for acceleration
To find the acceleration (a), rearrange the equation:
a=Fnetm=50N25kg=2m/s2
Conclusion
The acceleration of the child sliding down the rope is 2m/s2.
---
The forces acting on the child are:
1. The gravitational force (weight) acting downwards, which can be calculated using the formula:
Fgravity=m⋅g
where m=25kg and g=10m/s2.
Substituting the values into the formula:
Fgravity=25kg⋅10m/s2=250N
The net force (Fnet) acting on the child can be calculated by subtracting the force of friction from the gravitational force:
Fnet=Fgravity−Ffriction=250N−200N=50N
According to Newton's second law, the net force is also equal to the mass of the child multiplied by its acceleration:
Fnet=m⋅a
Substituting the known values:
50N=25kg⋅a
To find the acceleration (a), rearrange the equation:
a=Fnetm=50N25kg=2m/s2
The acceleration of the child sliding down the rope is 2m/s2.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-C)
63 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE
70 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A child weighing 25 kg slides down a rope hanging from the branch of a tall tree. If the force of friction acting against him is 2 N , what is the acceleration of the child
View SolutionA fireman of mass 60 kg slides down a pole. As shown in figure. He is pressing the pole with a force of 600 N. The coefficient of friction between the hands and the pole is 0.5. With wht acceleration will the fireman slide down (g=10m/s2)
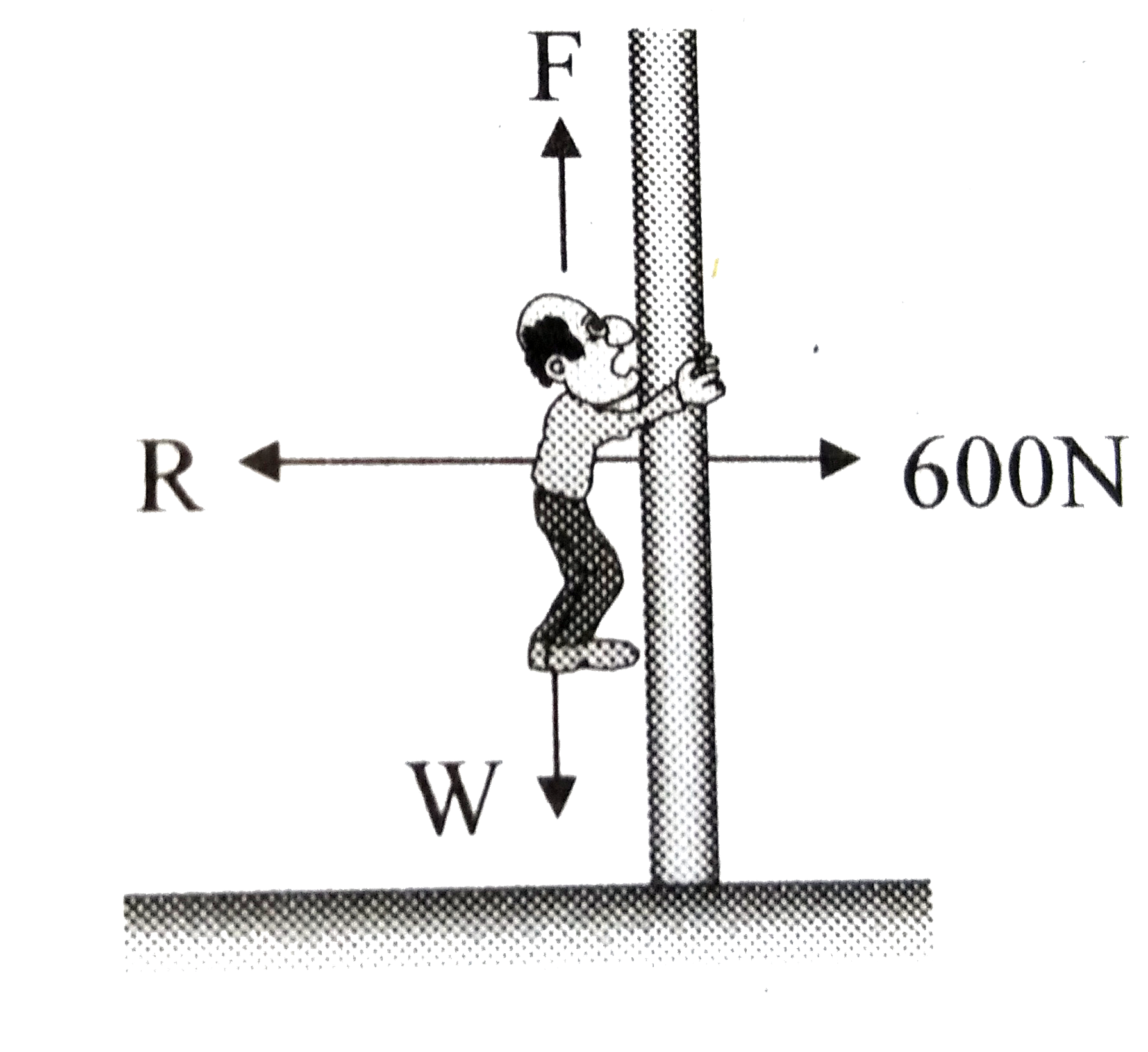
View Solution
Knowledge Check
A block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .
 A5.73m/sec2B8.0m/sec2C3.17m/sec2D10.0m/sec2
A5.73m/sec2B8.0m/sec2C3.17m/sec2D10.0m/sec2A block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
A98 JB72 JC56 JD34 JThe frictional force of the air on the body of mass 0.25kg, falling with an acceleration of 9.2 m/s2 will be (g=9.8m/s2).
A1.0NB0.55NC0.25ND0.15N
A stone weighing 1 kg and sliding on ice with a velocity of 2 m / s is stopped by friction in 10 sec . The force of friction (assuming it to be constant) will be
View SolutionA lorry of mass 2000 kg is traveling up a hill of certain height at a constant speed of 10 m/s. The frictional resistance is 200 N, then the power expended by the coolie is : (g=10m/s2)
View SolutionA monkey climbs up and another monkey climbs down a rope hanging from a tree with same uniform acceleration separately. If the respective masses of monkeys are in the ratio 2:3, the common acceleration must be
View SolutionA fireman of mass 60 kg slides down a pole. He is pressing the pole with a force of 600N. The coefficient of friction between the hands and the pole is 0.5, with what acceleration will the fireman slide down (g=10ms2)
View SolutionA man weighing 60 kg is in a lift moving down with an acceleration of 1.8 ms−2. The force exerted by the floor on him is
View Solution
