f(x)=x3at x=0 has inflection point y''=0 at x=0 and change sign.
Step by step video & image solution for f(x)=x^3a t\ x=0 has inflection point y ' '=0 at x=0 and change sign. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
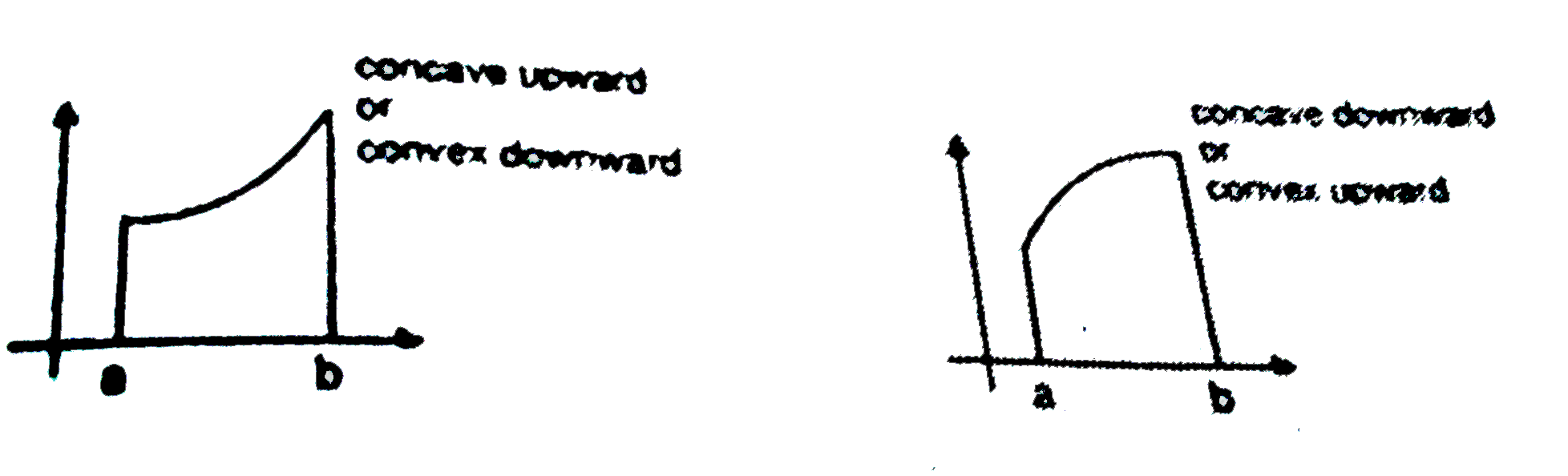
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)

Exhaustive set of values of 'a' for which the function f(x)=x4+ax3+3x22+1 will be concave upward along the entire real line is :A[−1,1]B[−2,2]C[0,2]D[0,4]Let f(x+y)−f(x)2=f(y)−12+xy, for all x,y∈R,f(x) is differentiable and f'(0)=1. Let g(x) be a derivable function at x=0 and follows the function rule g(x+yk)=g(x)+g(y)k,k∈R,k≠0,2andg'(0)−λg'(0)≠0.
If the graphs of y=f(x)andy=g(x) intersect in coincident points then λ can take valuesA-3B1C-1D4Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
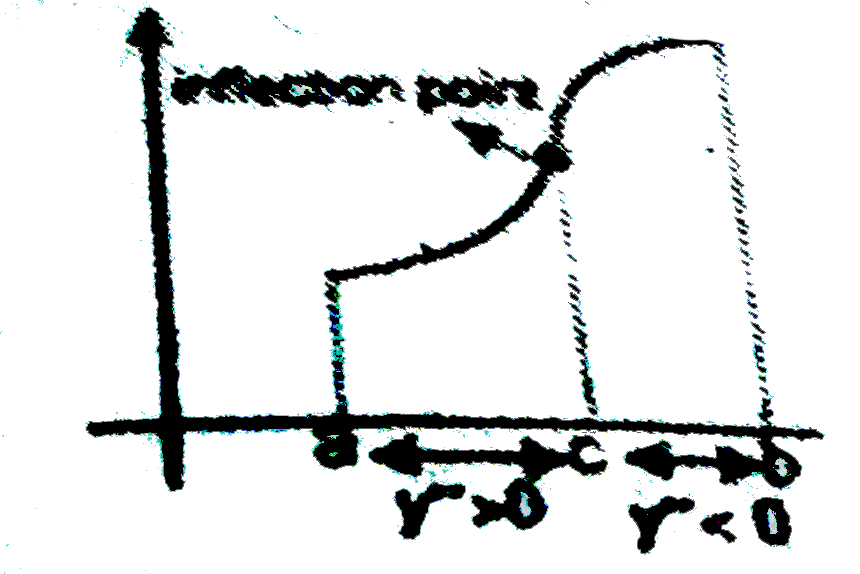
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :A1B2C3D4
The graph of the derivative f of a continuous function f is shown with f(0)=0

If f(x) has local minima at x=x1 and x=x2,f has inflection point at x=k, number of critical points of y=f(x) is w then x1+x2−k−w is...........
View SolutionThe function f(x)=x13(x−1) has two inflection points has one point of extremum is non-differentiable has range [−3x2−83,∞)
View SolutionThe curve f(x)=x23 ,at the point with x=0 ,has
View SolutionThe diagram shows the graph of the derivative of a functin f(x) for 0≤x≤4 with f(0) = 0. Which of the following could be correct statements for y = f(x)?
(##CENGRAC01S01021_Q01.png width=80%><br>(a)Tan≥ntl∈e→y=f(x)atx=0makesan∠of sec^(-1) sqrt 5 with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two.
View SolutionIf f(x)=|xaaaxaaax|=0, then f′(x)=0andfx=0 has common root fx=0andf′(x)=0 has common root sum of roots of f(x)=0 is −3a none of these
View Solution
