The median AD of ΔABC is prodiced upto X such that AD= DX. Prove that □ABXC is a parallelogram.
In ΔABC, since D is the mid-point of BC
∴AD=DCandAD=DX
Now, in quadrilateral ABXC,
AD=DX and BD = DC
i.e., its diagonals bisect each other.
Therefore, □ABXC is a parallelogram.

Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
Similar Questions
Knowledge Check
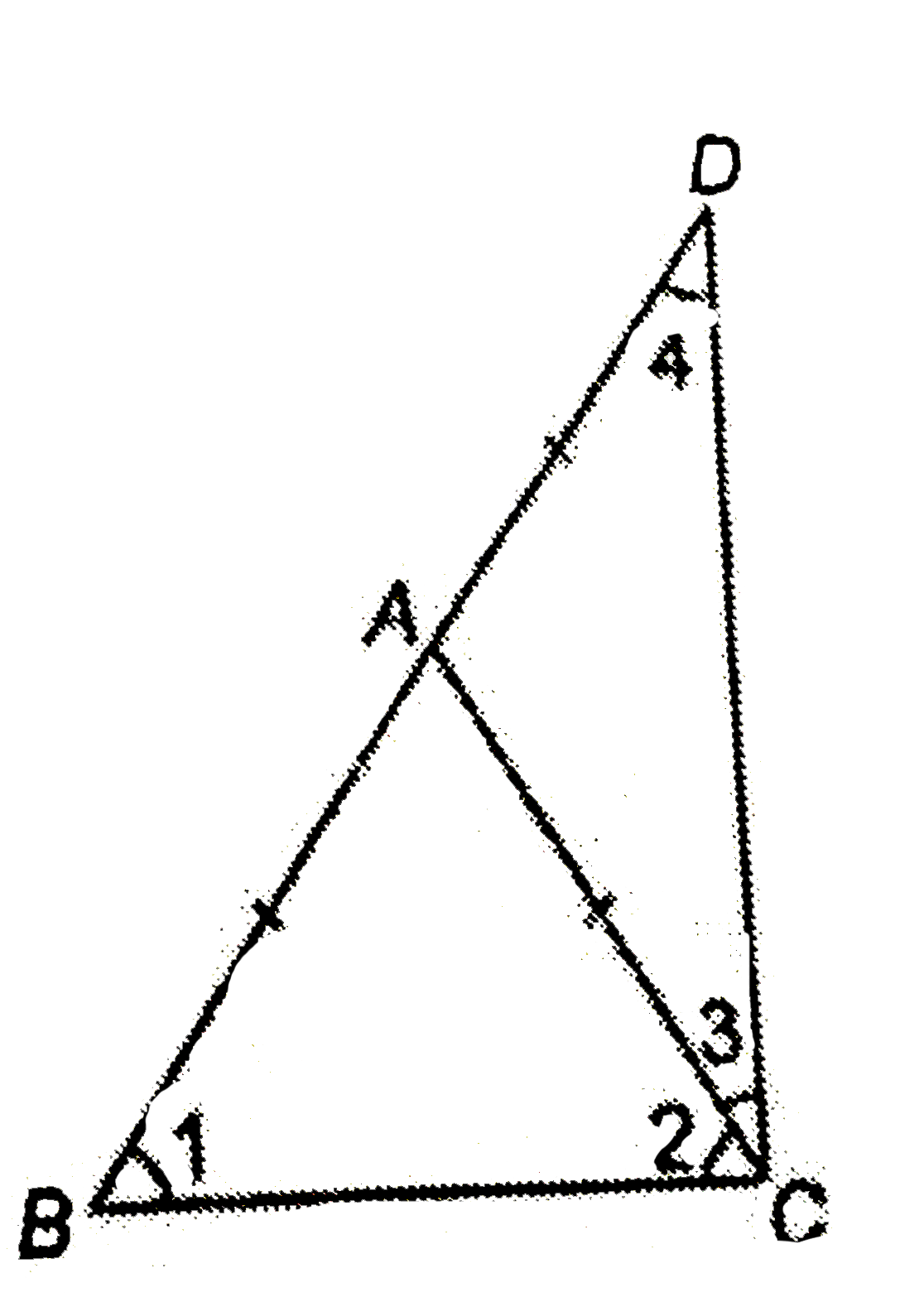
Assertion : In ABC, median AD is produced to X such that AD = DX. Then ABXC is a parallelogram.
Reason : Diagonals AX and BC bisect each other at right angles.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.E is a mid-point of median AD of ΔABC. BE is extended to meet AC at F. In what ratio AC is divided by F.
A2:3B2:1C1:3D3:2
D is a point on the base BC of ΔABC.AD is produced upto E such that DE = AD. Prove that:
area of ΔBCE= area of ΔABC
View SolutionΔABC is an isosceles triangle with AB = AC.
Side BA is produced to D such that AB = AD.
Prove that ∠BCD is a right angle.
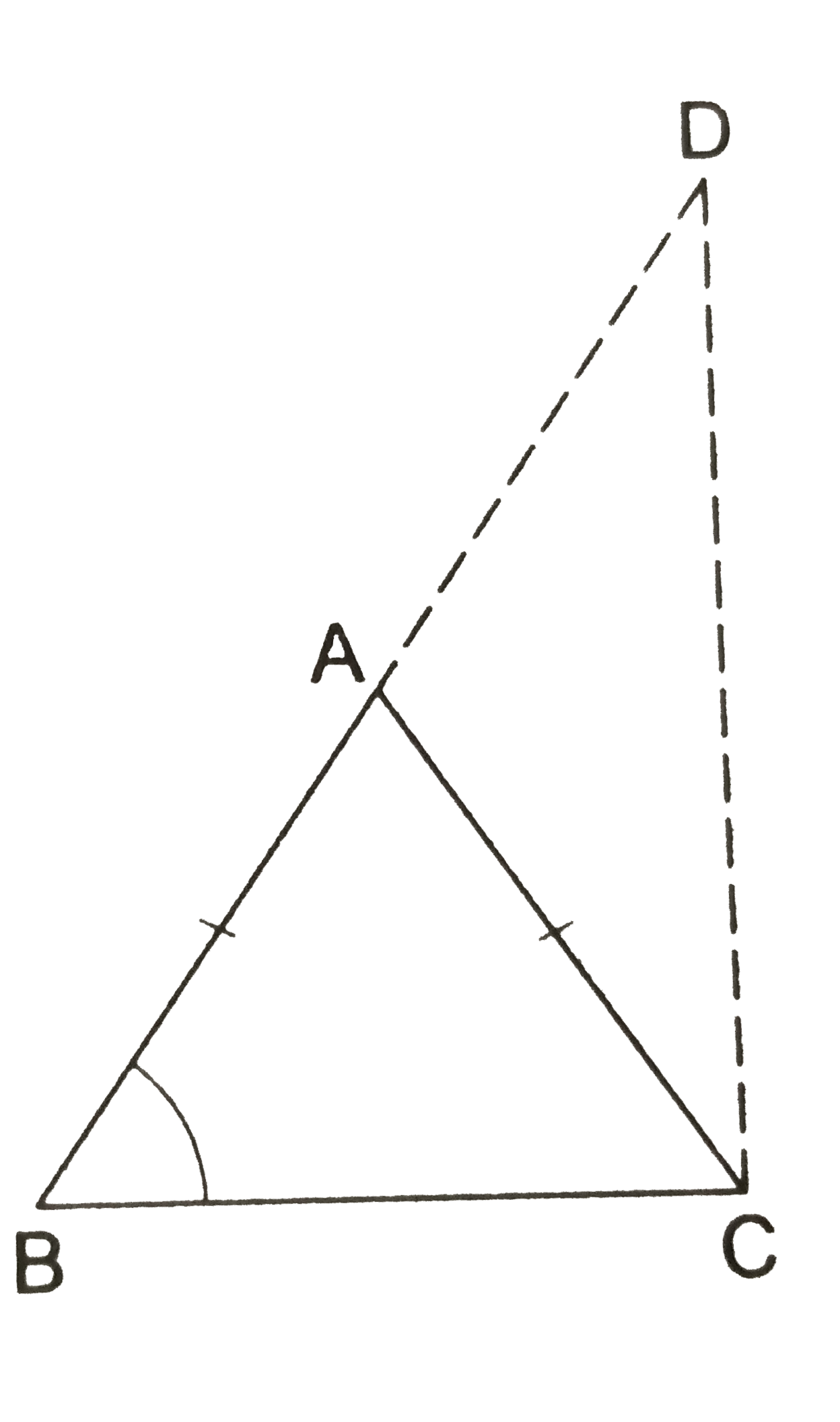
View SolutionΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13AD and Q is a point on BC such that CQ=13BP . Prove that AQCP is a parallelogram.
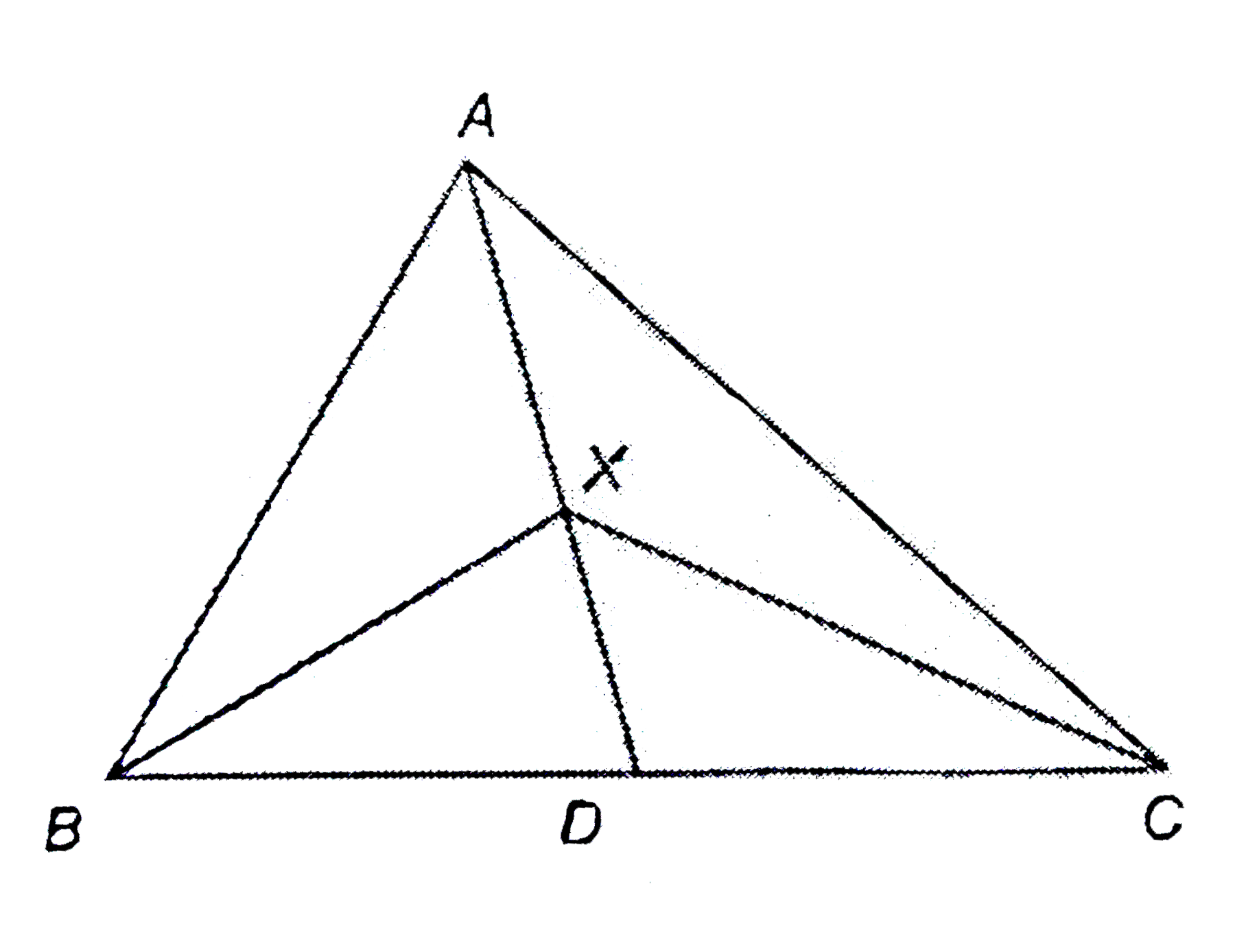
View SolutionIn the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)
View SolutionIn a ΔABC,D in mid-point of BC, AD is produced upto E so that DE=AD, prove that :
(i) ΔABD and ΔECD are congruent (ii) AB=EC
(iii) AB is parallel to EC.
View Solution
