In a ΔABC,D in mid-point of BC, AD is produced upto E so that DE=AD, prove that :
(i) ΔABD and ΔECD are congruent (ii) AB=EC
(iii) AB is parallel to EC.
To solve the problem, we will follow the steps outlined in the video transcript and provide a detailed explanation for each part of the question.
Given:
- Triangle ΔABC
- D is the midpoint of BC
- AD is extended to E such that DE=AD
To Prove:
(i) ΔABD≅ΔECD
(ii) AB=EC
(iii) AB∥EC
Step 1: Identify the Congruent Triangles
Since D is the midpoint of BC, we have:
- BD=DC (1)
From the problem, we know:
- AD=DE (2)
Also, the angles ∠ADB and ∠CDE are vertically opposite angles, which means:
- ∠ADB=∠CDE (3)
Step 2: Apply the SAS Congruence Criterion
Now we have:
1. BD=DC (from (1))
2. AD=DE (from (2))
3. ∠ADB=∠CDE (from (3))
Using the Side-Angle-Side (SAS) congruence criterion, we can conclude:
- ΔABD≅ΔECD
Step 3: Prove AB=EC
By the property of congruent triangles (CPCTC - Corresponding Parts of Congruent Triangles are Congruent), we have:
- AB=EC
Step 4: Prove AB∥EC
Since ΔABD≅ΔECD, we know:
- ∠ABD=∠ECD (from CPCTC)
These angles are alternate interior angles with respect to the transversal BC. Therefore, if two lines are cut by a transversal and the alternate interior angles are equal, then the lines are parallel:
- AB∥EC
Conclusion:
We have proved all parts of the question:
(i) ΔABD≅ΔECD
(ii) AB=EC
(iii) AB∥EC
- Triangle ΔABC
- D is the midpoint of BC
- AD is extended to E such that DE=AD
(i) ΔABD≅ΔECD
(ii) AB=EC
(iii) AB∥EC
Since D is the midpoint of BC, we have:
- BD=DC (1)
- AD=DE (2)
- ∠ADB=∠CDE (3)
Now we have:
1. BD=DC (from (1))
2. AD=DE (from (2))
3. ∠ADB=∠CDE (from (3))
- ΔABD≅ΔECD
By the property of congruent triangles (CPCTC - Corresponding Parts of Congruent Triangles are Congruent), we have:
- AB=EC
Since ΔABD≅ΔECD, we know:
- ∠ABD=∠ECD (from CPCTC)
- AB∥EC
We have proved all parts of the question:
(i) ΔABD≅ΔECD
(ii) AB=EC
(iii) AB∥EC
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7b15videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)10videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar5videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)10videos
SURFACE AREA AND VOLUME
Similar Questions
In a triangle ABC, D is mid-point of BC; AD is produced upto E so that DE = AD Prove that: (i) △ABDand△ECDare congruent. (ii) AB = EC. (ii) AB is parallel to EC
View SolutionD is a point on the base BC of ΔABC.AD is produced upto E such that DE = AD. Prove that:
area of ΔBCE= area of ΔABCView SolutionIn ABC, side AB is produced to D so that BD=BC. If ∠B=600 and ∠A=700, prove that: AD>CD (ii) AD>AC
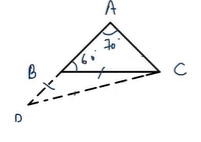 View Solution
View SolutionΔABC is an isosceles triangle with AB=AC, side BA is produced to D such that AB=AD. Prove that ∠BCD is a right angle.
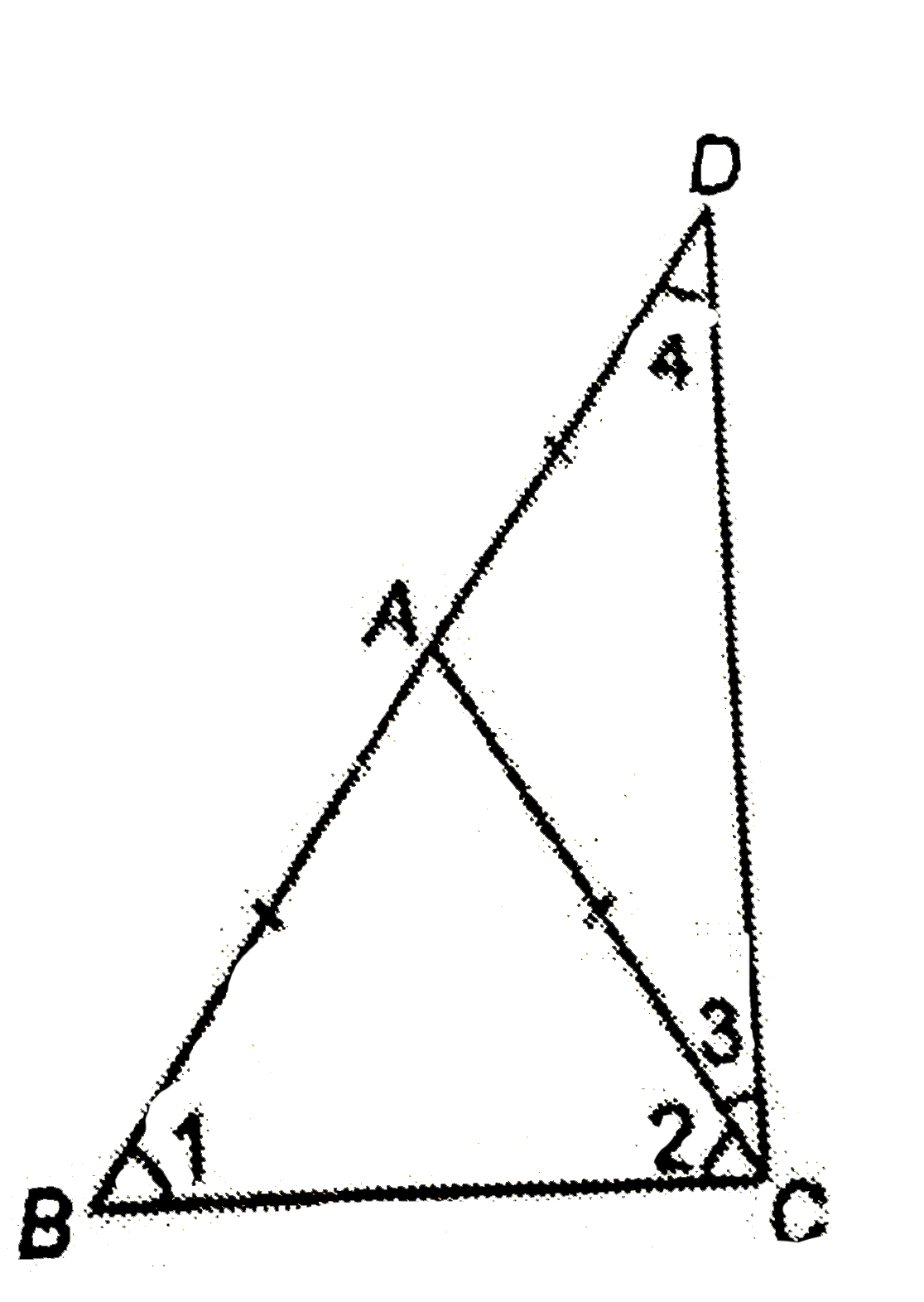 View Solution
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2ADView SolutionΔABC is an isosceles triangle with AB = AC.
Side BA is produced to D such that AB = AD.
Prove that ∠BCD is a right angle.
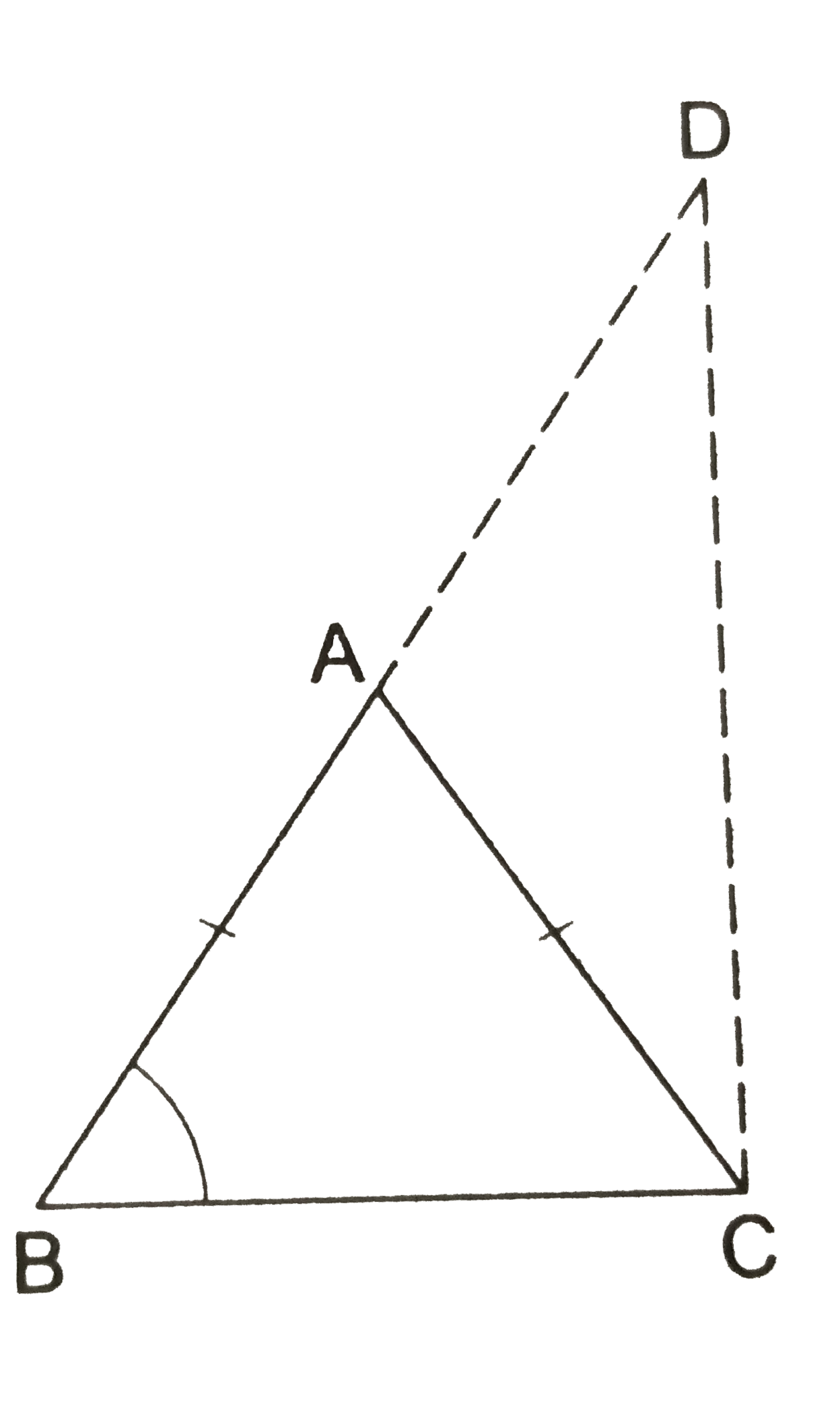 View Solution
View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn a tringle ABC, AB = AC and bisector of angle A meets BC at D. Prove that :
(i) ΔABD≅ΔACD (ii) AD is perpendicular to BC.View SolutionIn ΔABC,point D is on side BC such that DC = 6, BC = 15. find
(i)A(ΔABD):A(ΔABC) and
(ii) A(ΔABD):A(ΔADC).
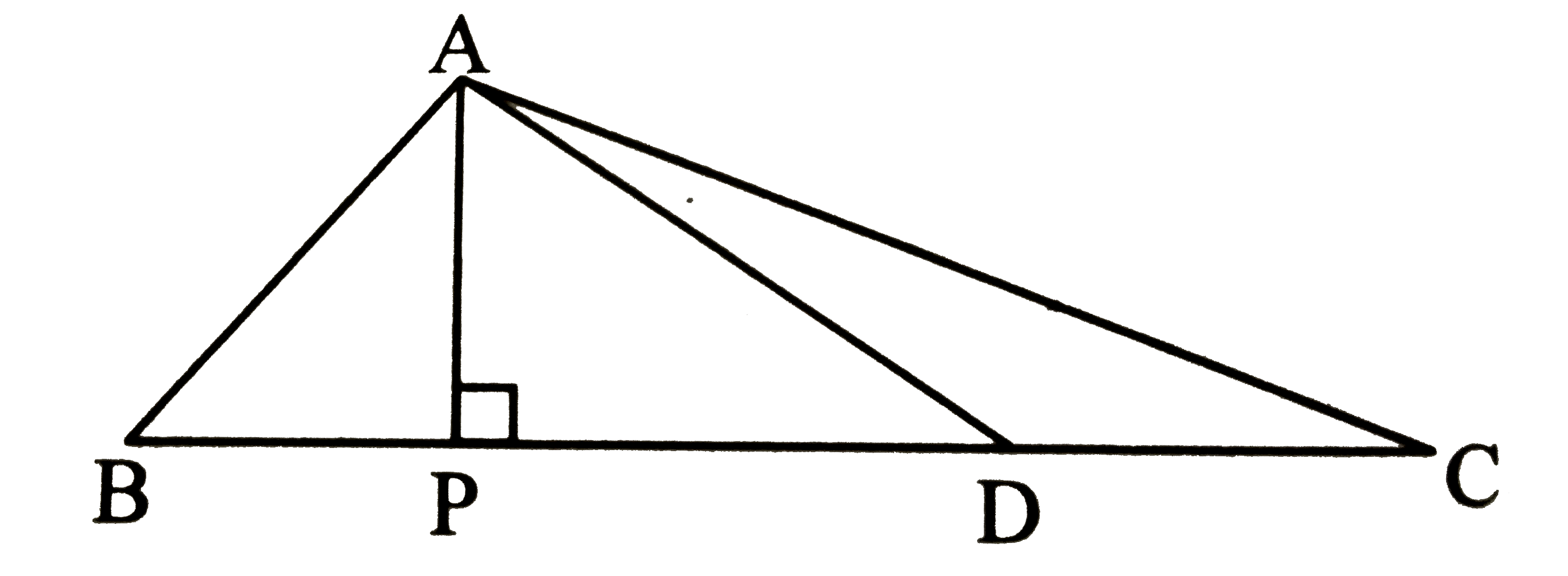 View Solution
View SolutionIn ΔABC,DandE two points on AB such that AD=BE. If DP||BCandEQ||AC, prove that such PQ∣∣AB.
 View Solution
View Solution

