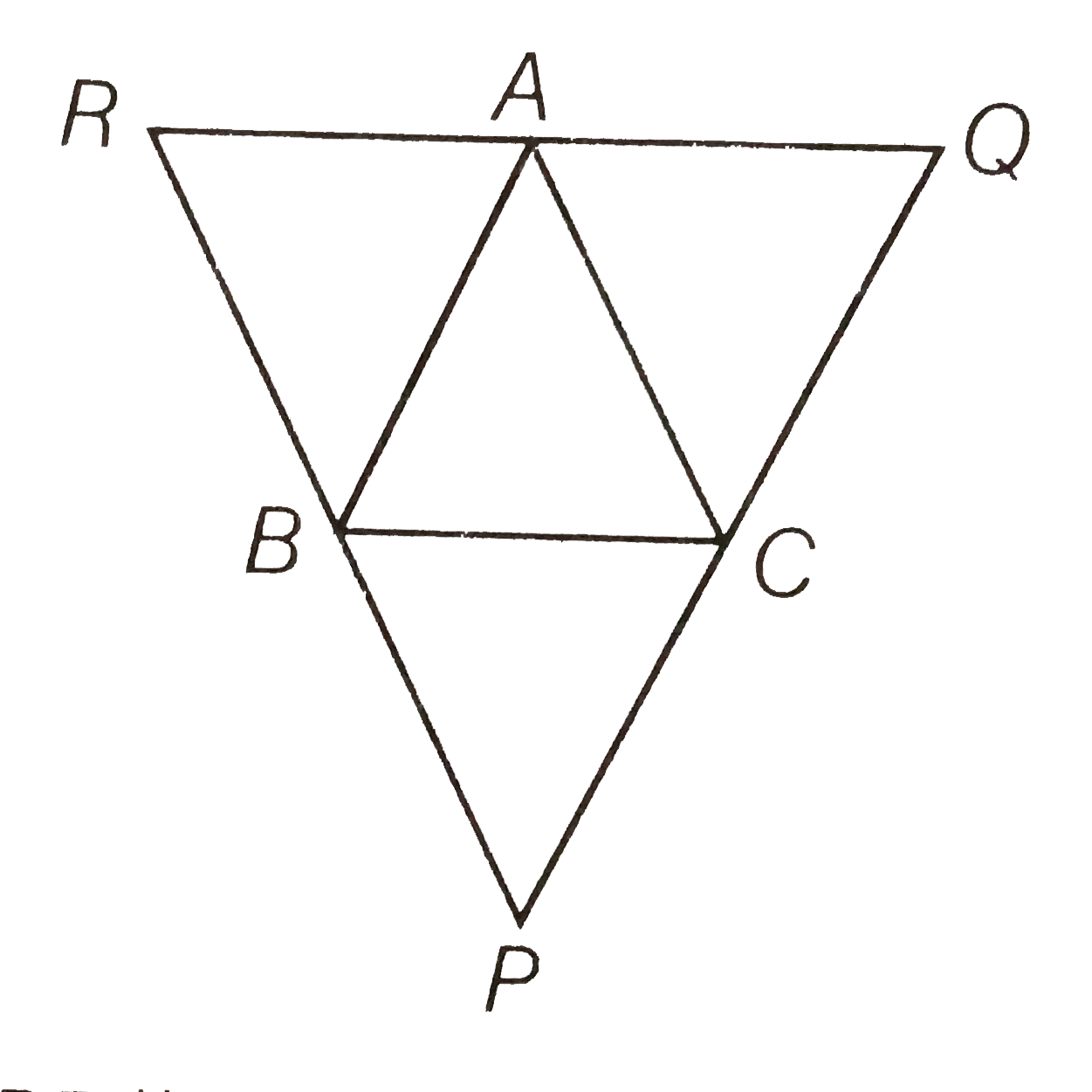
Throuth A,B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC. CA and AB of a ΔABC as shown in the given figure. Show that BC=12QR.
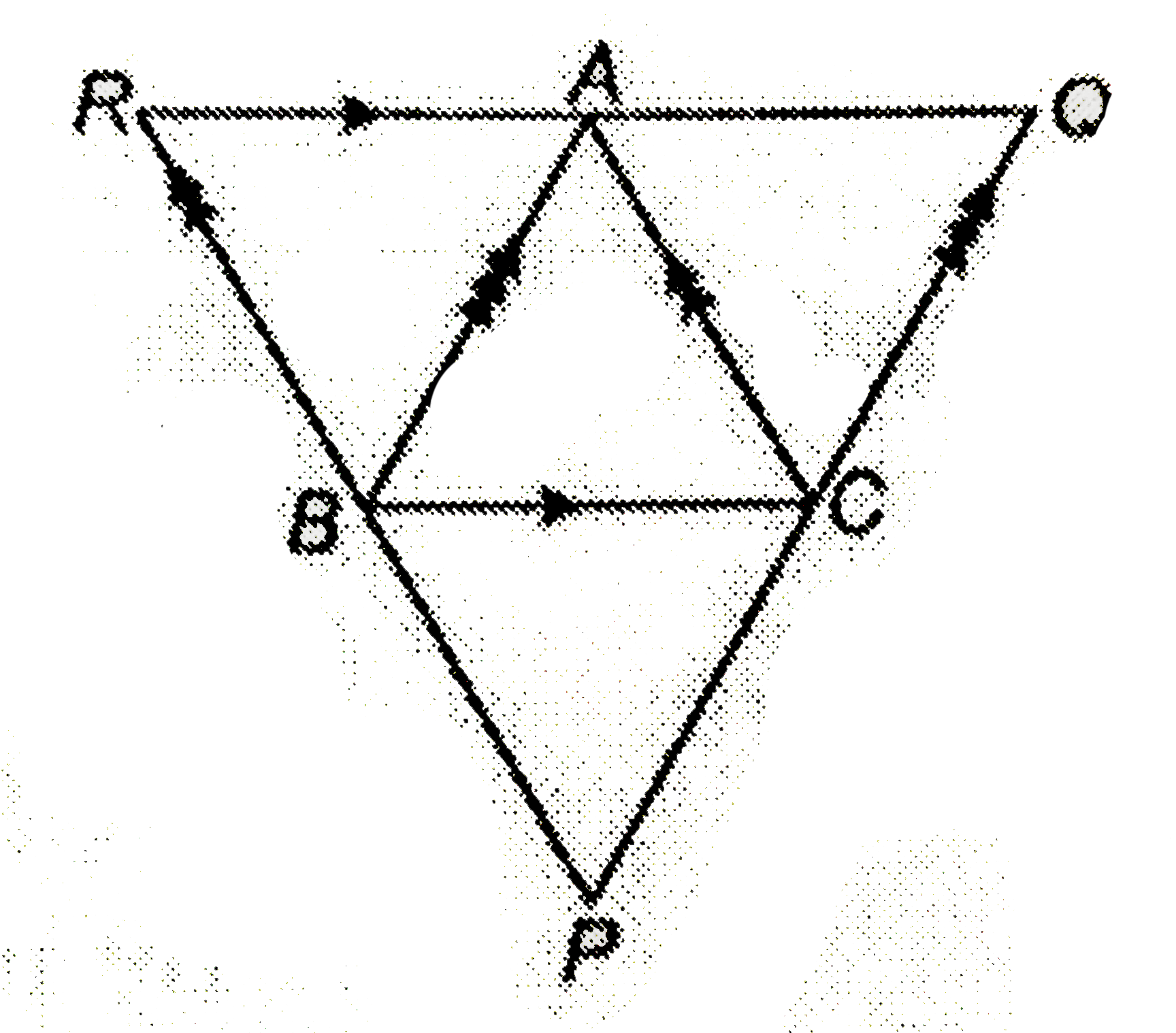
Given : Tringles ABC and PQR in which AB||QP,BC||RQandCA||PR.
To prove : BC=12QR
Proof: SinceRA||BCandBR||CA (given)
∴Quadrilateral RBCA is a parallelogram. (pair of opposite sides are parallel)
∴ RA=BC (∵opposite sides of a parallelogram)...(1)
Now, quadrilateral ABQA is a parallelogram.
∴ AQ=BC (∵opposite sides of a parallelogram)...(2)
Adding (1) and (2), we get
RA+AQ=2BC
⇒ QR=2BC
⇒ BC=12QR
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a29videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b15videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (long Answer Questions)5videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise10videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
If the vectors ¯a,¯b and ¯c from the sides BC, CA and AB, respectively, of ΔABC, then
A¯a.¯b+¯b.¯c+¯c.¯a=0B¯aׯb=¯bׯc=¯cׯaC¯a.¯b=¯b.¯c=¯c.¯aD(¯aׯb)+(¯bׯc)+(¯cׯa)=¯0
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(△DEF)=14ar(△ABC)View SolutionGiven ΔABC, lines are drawn through A,BandC parallel respectively to thesides BC,CAandAB, forming ΔPQR (Fig. 13.27). Show that BC=12QR.
View SolutionIf A,B and C are three points on a line and B lies between A and C (as shown in the given figure), then prove that AB+ BC= AC
View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
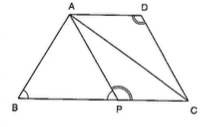
View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through AandC, lines are drawn parallel to BCandPA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
 View Solution
View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through A and C, lines are drawn parallel to BC and PA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2ADView Solution