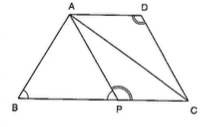
P
is a point on the side BC
of a triangle ABC
such that AB=AP.
Through AandC,
lines are drawn parallel to BCandPA,
respectively, so as to intersect at D
as shown in Figure. Show that ABCD
is a cyclic quadrilateral.
Step by step video & image solution for P is a point on the side B C of a triangle A B C such that A B=A Pdot Through Aa n dC , lines are drawn parallel to B Ca n dP A , respectively, so as to intersect at D as shown in Figure. Show that A B C D is a cyclic quadrilateral. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
P is a point on the side BC of a triangle ABC such that AB=AP. Through AandC, lines are drawn parallel to BCandPA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.

View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through A and C, lines are drawn parallel to BC and PA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
View SolutionABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively intersecting at P, Q and R . Prove that the perimeter of PQR is double the perimeter of ABC
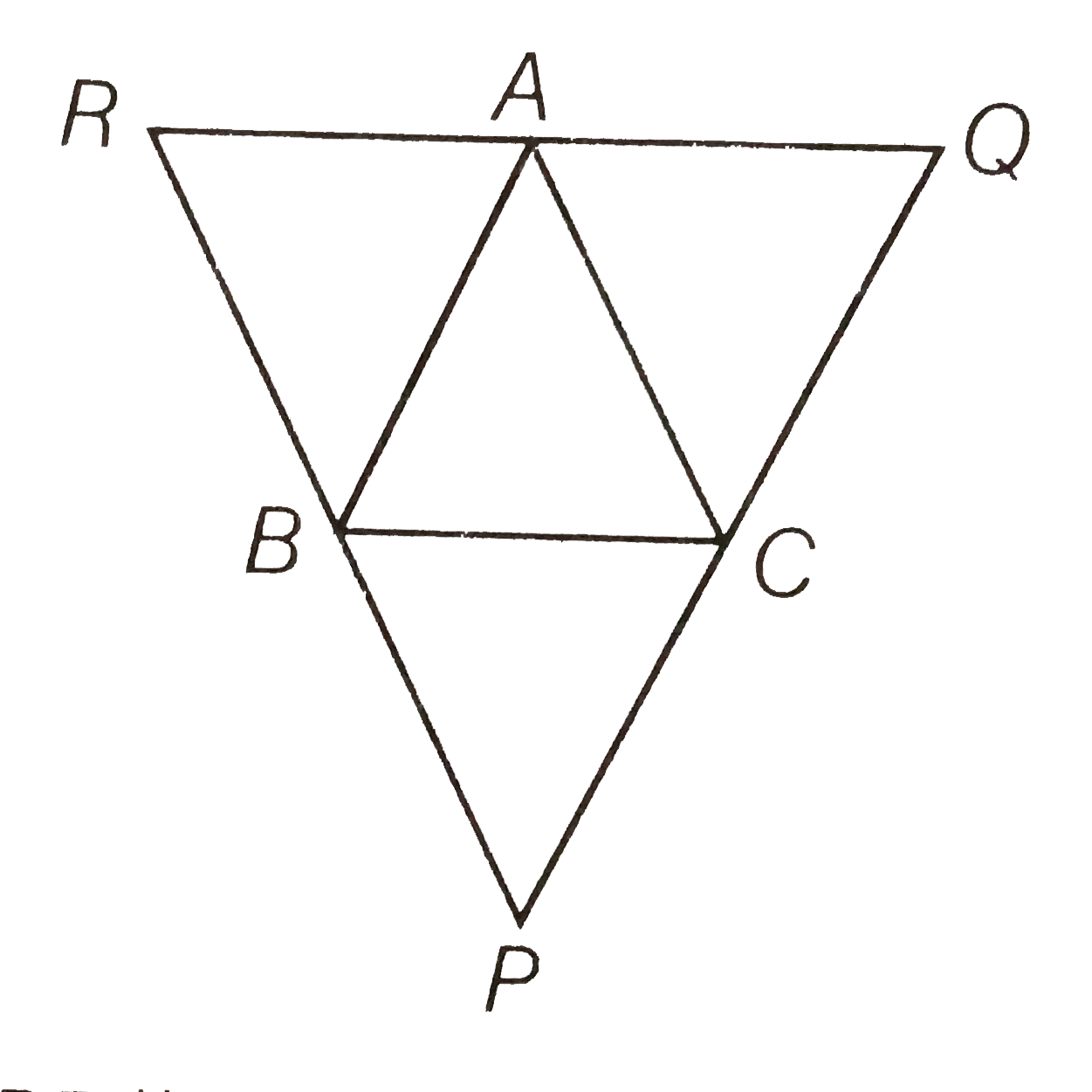
View SolutionThrough A, B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ΔABC as shown in figure. Show that BC=12QR.
View SolutionTwo tangents PAandPB are drawn from an external point P to a circle with centre O. Prove that AOBP is a cyclic quadrilateral.
View SolutionGiven ABC , lines are drawn through A, B and C parallel respectively to the sides BC, CA and AB, forming PQR.Figure .Show that BC=12QR
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(^(gm)ABCD)=argmPBQR).

View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in Figure. Prove that ar (ABP)=ar (Qua..ABCD).
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionP is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. If AD=10cm, then CD= 5cm (b) 6cm (c) 8cm (d) 10cm
View Solution
