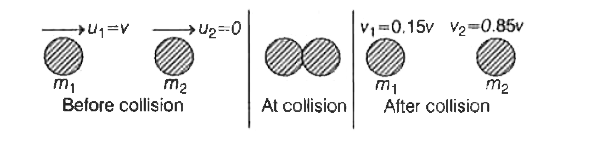
A ball moving with a velocity v, colliders head on with a stationary second ball of same mass.
After the collision, the velocity of the first ball is reduced to 0.15 v. The kinetic energy of the system is decreased nearly bySolution in Telugu

A

0.2

B

0.25

C

0.3

D

0.4

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Given,

$\Rightarrow$ Momentum is conserved,
$m_{1} u_{1} + m_{2} u_{2} = m_{1} v_{1} + m_{1} v_{2}$
Given $m_{1} = m_{2} = m, u_{1} = v and u_{2} = 0,$
also v = 0.15 v
$m v = m (0, 15 v) + m v_{2}$
$v - 0.15 v = v_{2}$
$\Rightarrow 0.85 v = v_{2}$ m / s ...(i)
Here, initial kinetic energy is
$\frac{1}{2} μ_{1}^{2} = \frac{1}{2} m v^{2}$ ...(ii)
Final kinetic energy is
$\frac{1}{2} m v_{1}^{2} + \frac{1}{2} m v_{2}^{2} = \frac{1}{2}, {(0.15 v)}^{2} + \frac{1}{2} m {(0.85 v)}^{2}$ ...(iii)
The decrement in kinetic energy is
$Δ K E = {(K E)}_{i} - {(K E)}_{f}$
$\Rightarrow Δ K E = \frac{1}{2} m v^{2} - [\frac{1}{2} m {(0.15 v)}^{2} + \frac{1}{2} m (0.85)]$
$Δ K E = \frac{1}{2} m v^{2} - [\frac{1}{2} m {(0.15 v)}^{2} + \frac{1}{2} m (0.85)]$ ...(iv)
% cahnge in kinetic energy $= \frac{Δ K E}{{(K E)}_{i}} \times 100$
$= \frac{\frac{1}{2} m v^{2} [1 - {(15)}^{2} - {(85)}^{2}]}{\frac{1}{2} m v^{2}}$
% decrease in KE = 25.5% = 25%

|

Updated on:21/07/2023

Class 12 PHYSICS ONLINE QUESTION PAPER 2018

Topper's Solved these Questions

Similar Questions

TS EAMCET PREVIOUS YEAR PAPERS-ONLINE QUESTION PAPER 2018-PHYSICS

Home
Ask Doubt
Profile