In the figure, pulleys are smooth and strings are massless, m1=1 kg and m2=13kg. To keep m3 at rest, mass m3 should be
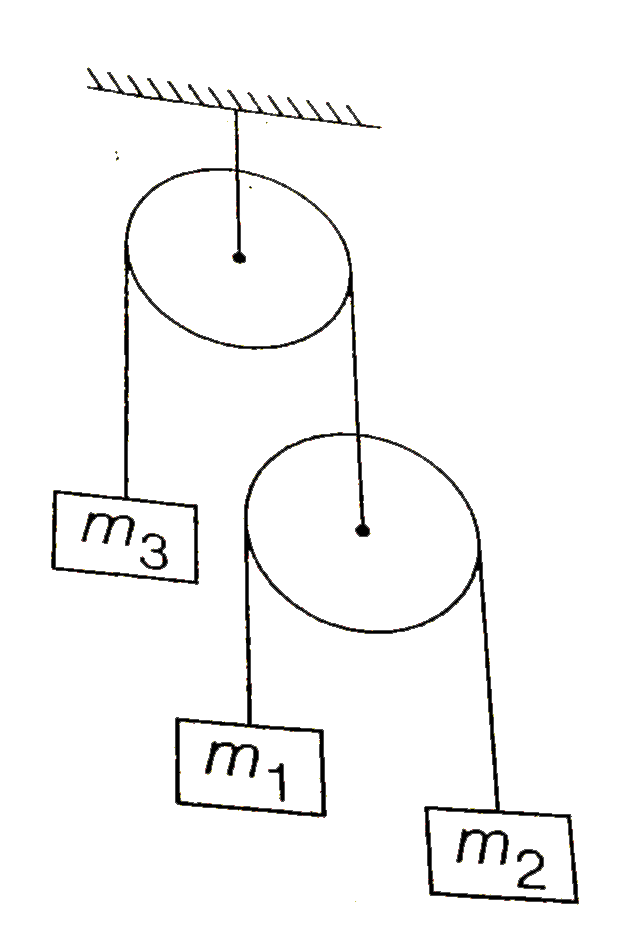
1 kg
23kg
14kg
2kg
The correct Answer is:A
(a) m3 is at rest, Therefore
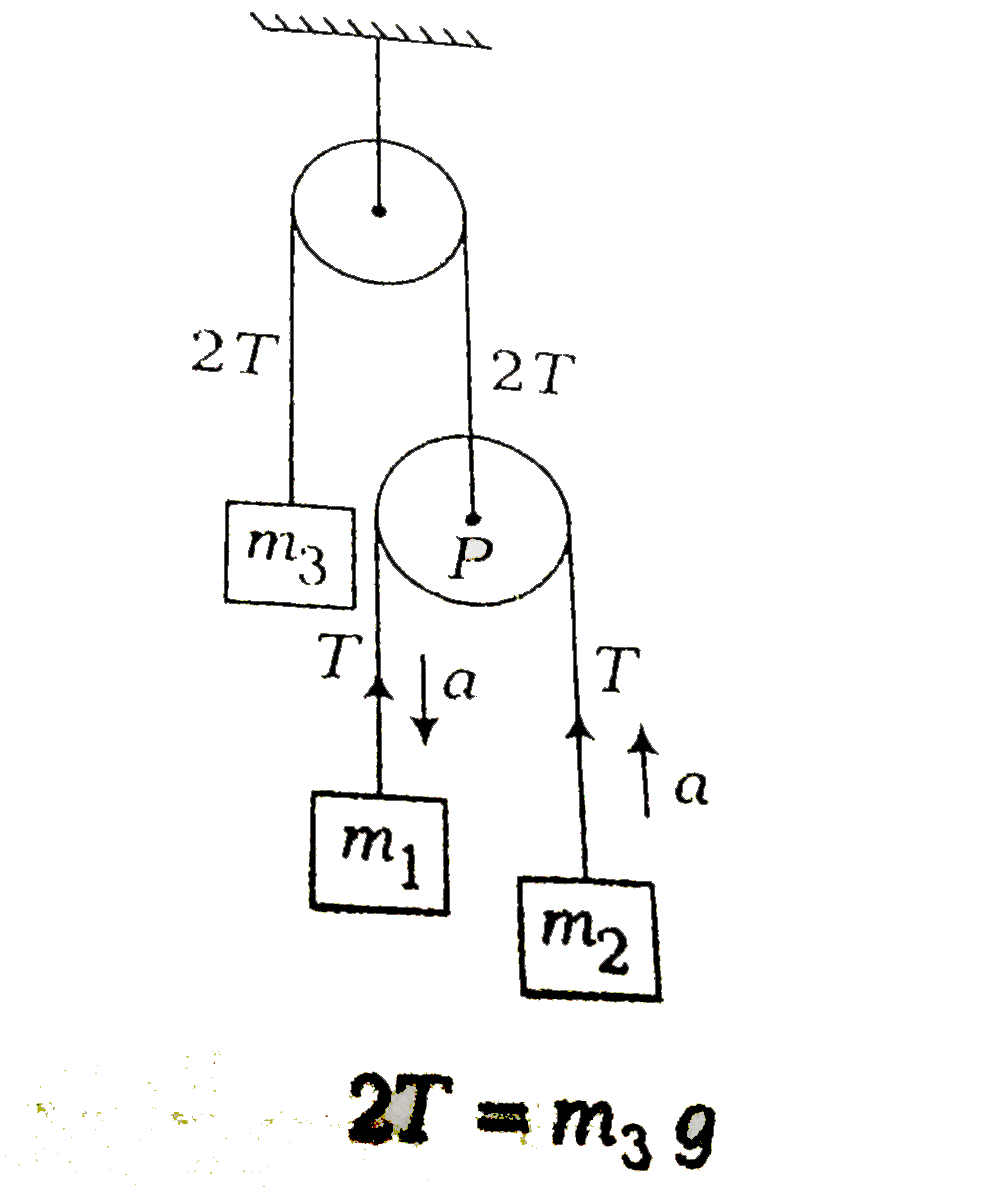
2T=m3g….(i)
Further if m3 is at rest, then pully P is also at rest. Writing equations of motion.
m1g−T=m1a ….(ii)
T−m2g=m2a ...(iii)
Solving Eq. (ii) and (iii) we get, m3=1kg
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Assertion and reason
28 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
Pulleys are ideal and string are massless. The masses of blocks are m1=4kg and m2=1kg as shown.If all surfaces are smooth then the acceleration of m2 in m/s2 is (g=10m/s2 )

View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
The acceleration of m3 is
View Solution
Knowledge Check
In the arrangement shown in the all contact surfaces are smooth strings and pulleys are massless
Given M1=1kg,M2=2kg,M3=4kg and g=10ms−2
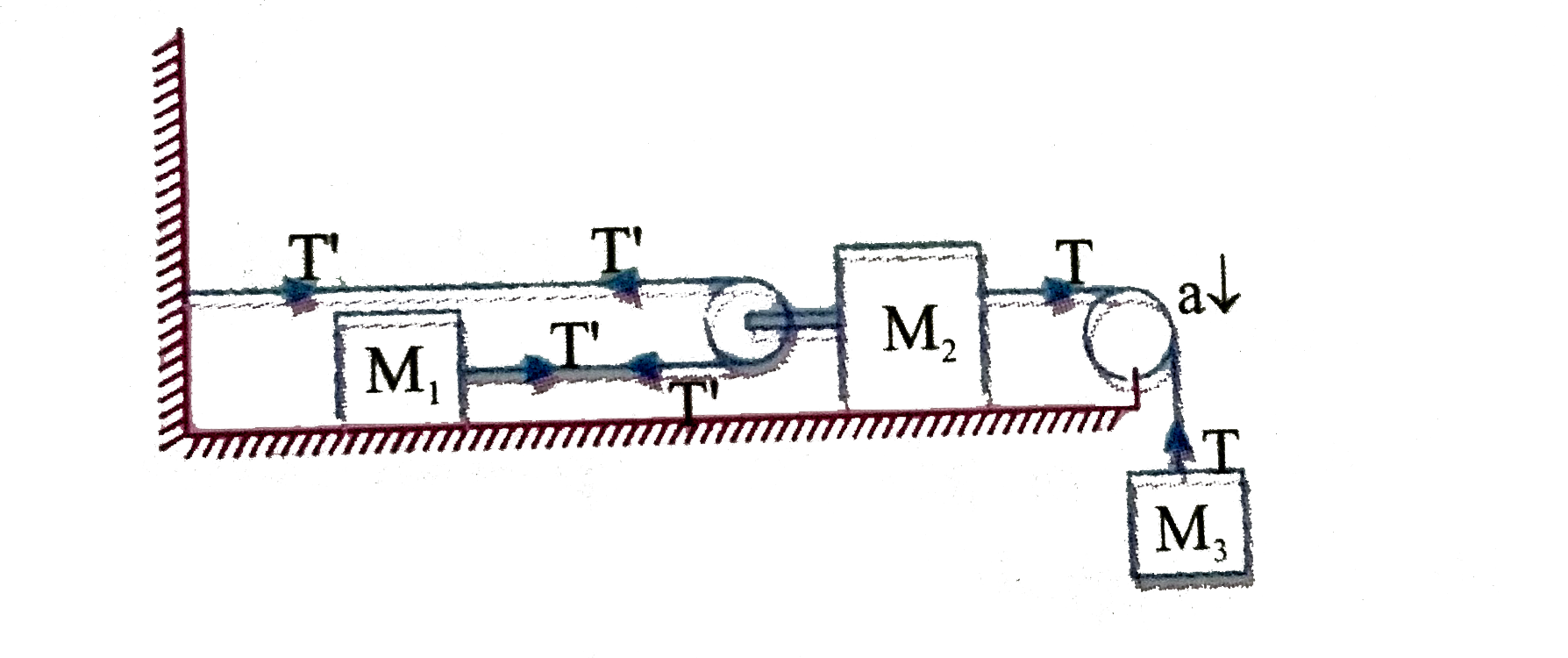 .AThe acceleration of block of mass M3 is 4ms−2BThe acceleration of block of mass M1 is 4ms−2CThe tension (T) in the string connecting blocks of masses M3 and M2 is 24N .DThe tension (T) in the string connecting blocks of masses M1 and M2 is 24N .
.AThe acceleration of block of mass M3 is 4ms−2BThe acceleration of block of mass M1 is 4ms−2CThe tension (T) in the string connecting blocks of masses M3 and M2 is 24N .DThe tension (T) in the string connecting blocks of masses M1 and M2 is 24N .M is a fixed wedge. Masses m1 and m2 are connected by a light string. The wedge is smooth and the pulley is smooth and fixed m1=10kg and m1=7.5kg . When m2 is just released, the distance it will travel in 2 second is.
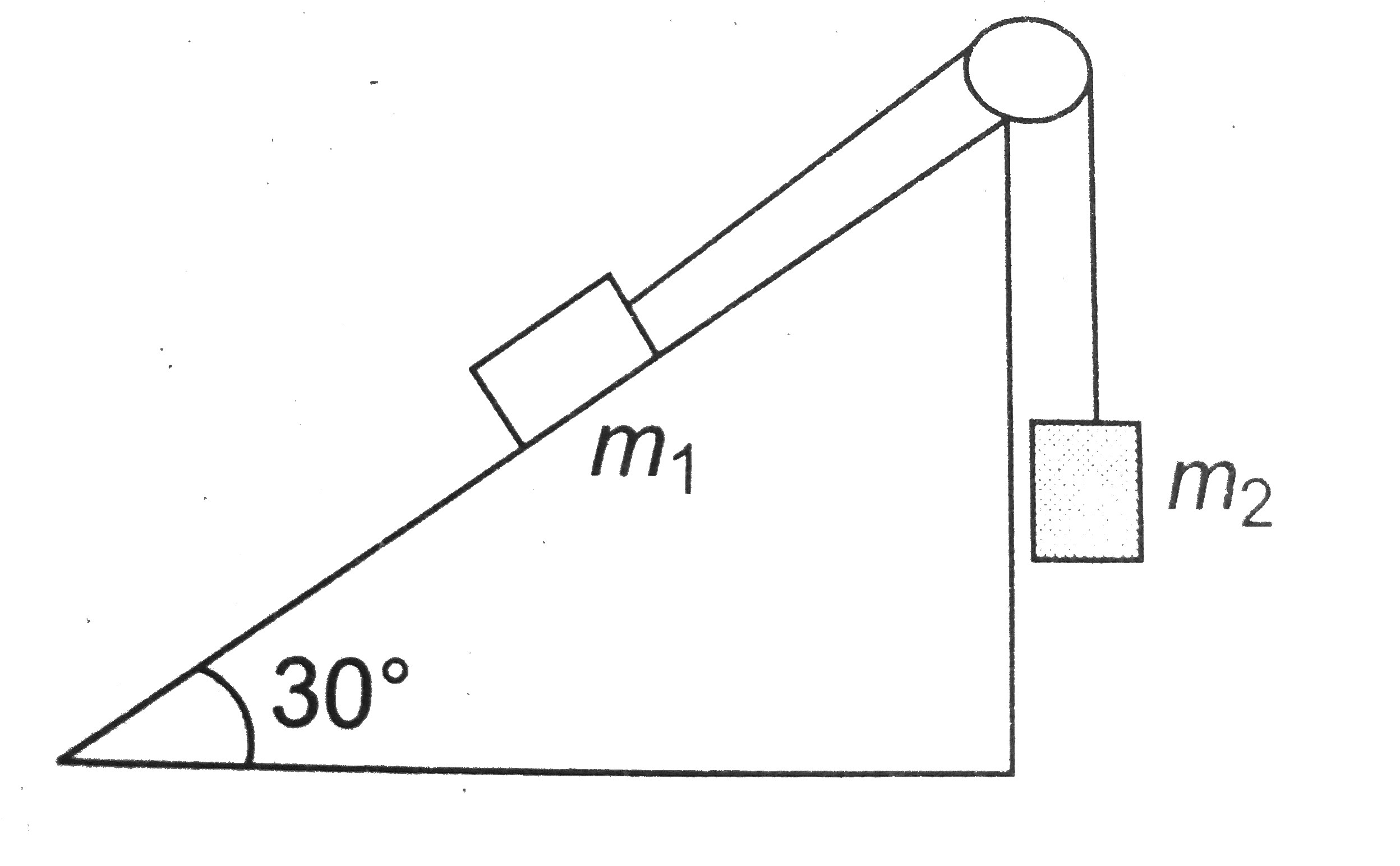 A2.8mB7.5mC4.0mD6.0m
A2.8mB7.5mC4.0mD6.0mIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
The acceleration of m3 isA407ms−2B307ms−2C207ms−2DNone of these
In fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
The acceleration of m1 is
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
Find the tension in the string
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
The acceleration of m1 is
View SolutionIn the adjacent figure, all the pulleys are frictioniess and massless, all the stringes are also massless. The relation between a1,a2 and a3 is (where a1,a2 and a3 are the acceleration of masses m1,m2 and m3 respectively in the direction as shown in the figure)
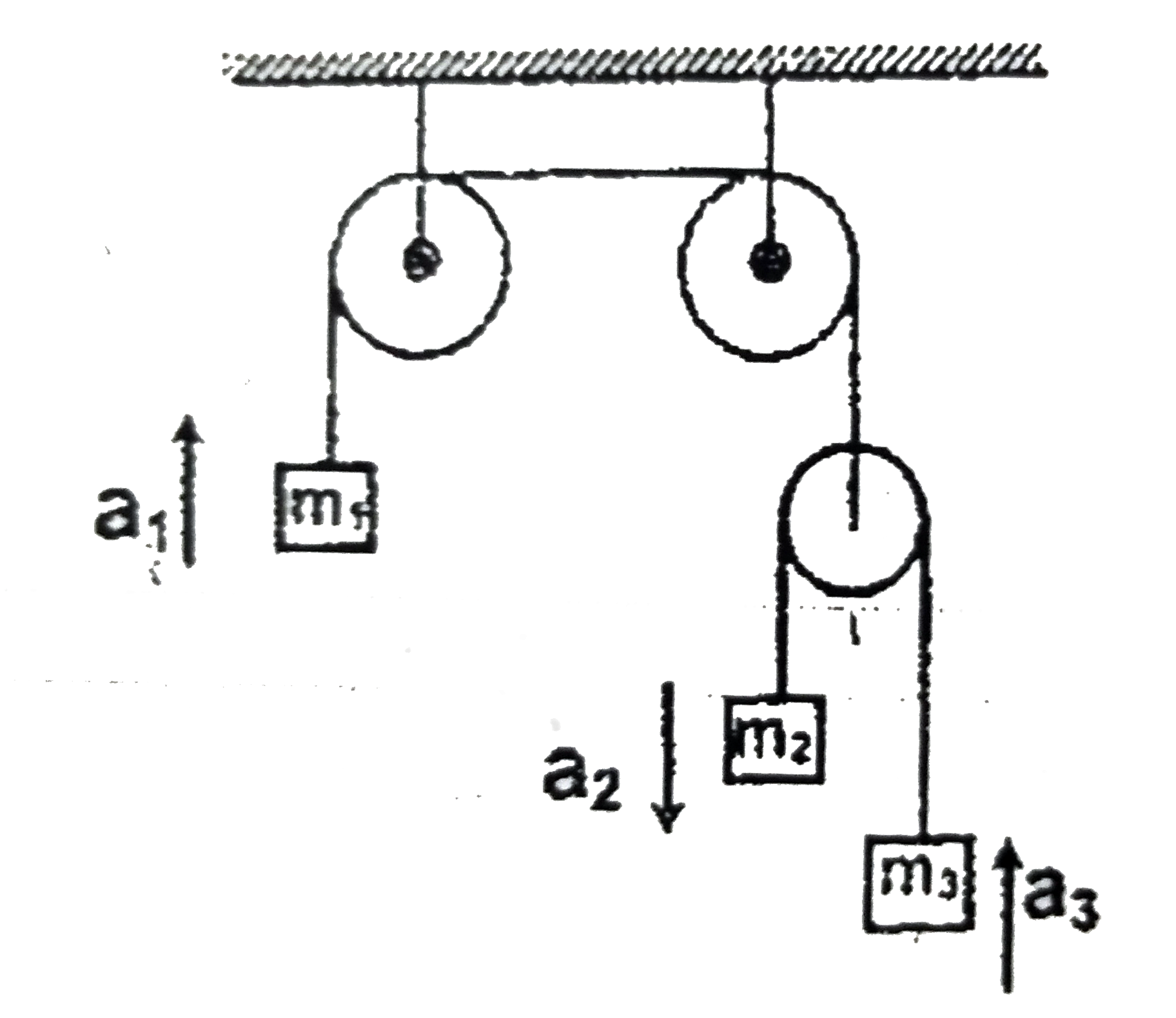
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
Find the tension in the string
View Solution
