In a spring- mass system , the length of the spring is L, and it has a mass M attached to it and oscillates with an angular frequency ω. The spring is then cut into two parts, one (i) with relaxed length αL and the other (ii) with relaxed length (1−α) L. The force constants of the two spring A and B are
k1−α and kα
kα and k1−α
αk,(1−α)k
k and k
The correct Answer is:B
(b)Force constant , k∝1Length of spring
∴kAk=LαL
∴kA=kα
Similarly, kB=k1−α
Similar Questions
If a spring of force constant 'k' is cut into two parts, such that one part is thrice in length of the other part. Then the force constant of each part are
View SolutionA spring having a spring constant k is loaded with a mass m. The spring is cut into two equal parts and one of these is loaded again with the same mass. The new spring constant i
View Solution
Knowledge Check
A spring has length'l' and spring constant 'k'. It is cut into two pieces of lengths l1andl2 such that l1=nl2. The force constant of the spring of length l1 is
Ak(l+n)BkCk(n+1)Dk(n+l)nA block of mass m, when attached to a uniform ideal apring with force constant k and free length L executes SHM. The spring is then cut in two pieces, one with free length n L and other with free length (1−n)L. The block is also divided in the same fraction. The smaller part of the block attached to longer part of the spring executes SHM with frequency f1 . The bigger part of the block attached to smaller part of the spring executes SHM with frequency f2. The ratio f1/f2 is
A1Bn1−nC1+nnDn1+nA small mass m attached to one end of a spring with a negligible mass and an unstretched length L, executes vertical oscillations with angular frequency ω0. When the mass is rotated with an angular speed ω by holding the other end of the spring at a fixed point, the mass moves uniformly in a circular path in a horizontal plane. Then the increase in length of the spring during this rotation is
Aω2Lω20−ω2Bω20Lω2−ω20Cω2Lω20Dω20Lω2
If a spring of spring constant K is vcut into two parts A and B having lengths in the ratio of 1 : 4 .Calculate the ratio of spring constants of Aand B .
View SolutionAn underformed spring with the spring constant k has length l0. When the system (Fig.) rotates at an angular
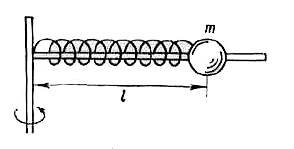
velocity ω, the weight with mass m causes an extension of the spring. Find the length l of the rotating spring.
View SolutionIf the system is suspended by the mass m the length of the spring is l1. If it is inverted and hung by mass M, the length of the spring is l2. Find the natural length of the spring.

View SolutionA spring of constant K is cut into two parts of length in the ratio 2:3 . The spring constant of large spring is
View SolutionA small mass m attached to one end of a spring with a negligible mass and an unstretched length L, executes vertical oscillations with angular frequency ω0 When the mass is rotated with an angular speed ω by holding the other end of the spring at a fixed point, the mass moves uniformly in a circular path in a horizontal plane. Then the increase in length of the spring during this rotation is
View Solution
