Given a ΔABD in which AB=AD and AC bisects BD. Prove that :
ΔABC≅ΔADC.
To prove that triangle ABC is congruent to triangle ADC, we will use the criteria for triangle congruence. Here are the steps:
Step 1: Identify the Given Information
We are given:
- Triangle ABD where AB = AD (sides are equal).
- Line AC bisects BD, meaning that point C divides BD into two equal segments, so BC = CD.
Step 2: Establish the Angles
Since AB = AD, by the Isosceles Triangle Theorem, we know that:
- Angle ABC = Angle ADC (the angles opposite the equal sides are equal).
Step 3: Identify the Common Side
The side AC is common to both triangles ABC and ADC:
- AC = AC (common side).
Step 4: Apply the Side-Angle-Side (SAS) Congruence Criterion
Now we have:
1. AB = AD (given)
2. Angle ABC = Angle ADC (from Step 2)
3. AC = AC (common side)
According to the SAS criterion, if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.
Conclusion
Thus, we can conclude that:
- Triangle ABC ≅ Triangle ADC.
We are given:
- Triangle ABD where AB = AD (sides are equal).
- Line AC bisects BD, meaning that point C divides BD into two equal segments, so BC = CD.
Since AB = AD, by the Isosceles Triangle Theorem, we know that:
- Angle ABC = Angle ADC (the angles opposite the equal sides are equal).
The side AC is common to both triangles ABC and ADC:
- AC = AC (common side).
Now we have:
1. AB = AD (given)
2. Angle ABC = Angle ADC (from Step 2)
3. AC = AC (common side)
Thus, we can conclude that:
- Triangle ABC ≅ Triangle ADC.
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7b
15 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
In the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
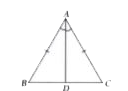
ΔADB≅ΔADC
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
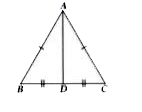 Prove that:
Prove that:
ΔADB≅ΔADC
View SolutionIn the adjoining figure, AD=DC and bisects ∠ADC. Prove that ΔADB≅ΔCDB.

View SolutionIn a tringle ABC, AB = AC and bisector of angle A meets BC at D. Prove that :
(i) ΔABD≅ΔACD (ii) AD is perpendicular to BC.
View SolutionIn the given figure, AB = AD and ∠1=∠2. Prove that : ΔABC≅ΔADC

View SolutionIn the given figure, AB∣∣EC,AB=AC and AE bisects ∠DAC. Prove that:
View SolutionIn the given figure, ΔABC is an isosceles triangle in which AB=AC and AE bisects ∠CAD. Prove that AE∣∣BC.
View SolutionIn the following figures, AB=PQ,AC=PR and AM=PN. Prove that ΔABC≅ΔPQR.
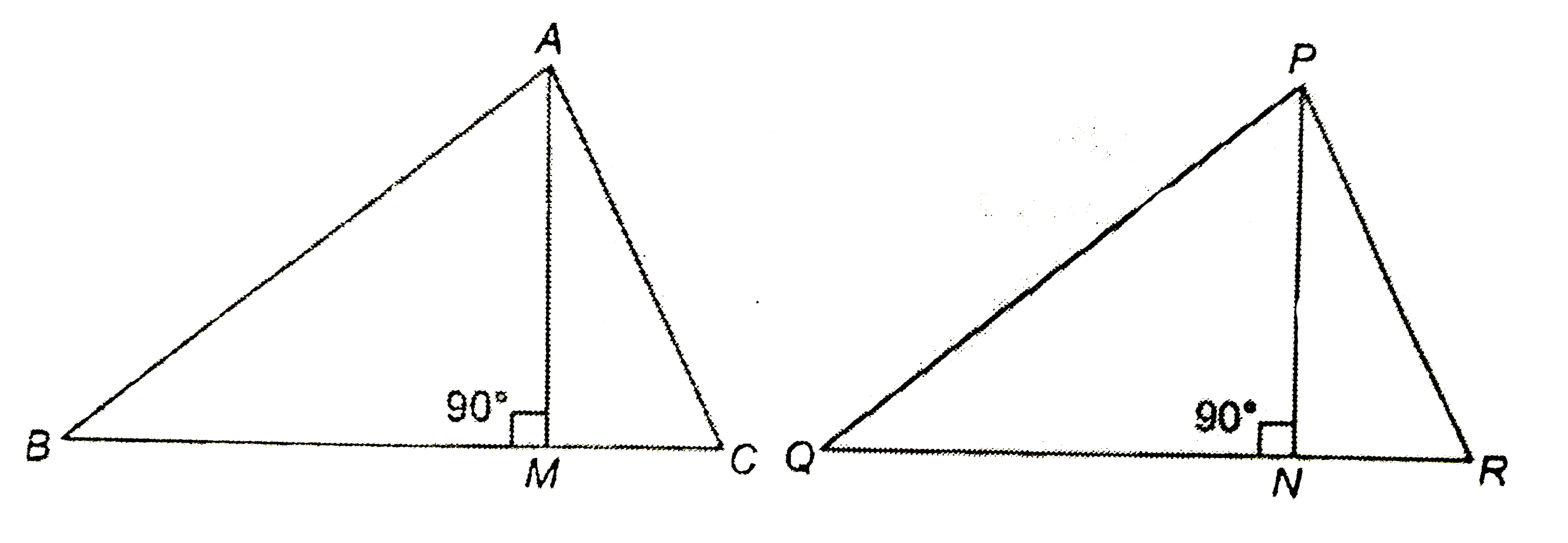
View SolutionABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA Prove that (i) ΔABD≅ΔBAC (ii) BD = AC (iii) ∠ABD=∠BAC
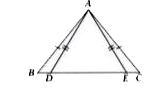
View SolutionIn the given figure, AB = AC and AD = AE. Prove that:
ΔABD≅ΔACE
View Solution
