Equilateral triangles ABD and ACE are drawn on sides AB and AC respectively of a outside it. Prove that :
(i) (ii)
To prove the given statements about the equilateral triangles ABD and ACE drawn on the sides AB and AC of triangle ABC, we will follow a systematic approach.
Given:
- Triangle ABC
- Equilateral triangle ABD on side AB
- Equilateral triangle ACE on side AC
To Prove:
1. ∠DAC=∠EAB
2. DC=BE
1. Identify Angles in Equilateral Triangles:
Since triangles ABD and ACE are equilateral, each angle in these triangles measures 60∘.
- Therefore, ∠ADB=60∘ and ∠AEC=60∘.
2. Relate Angles:
We know that:
- ∠DAB=∠EAC=60∘ (since they are angles of equilateral triangles).
3. Add Angles:
Now, consider the angles ∠DAC and ∠EAB:
∠DAC=∠DAB+∠BAC
∠EAB=∠EAC+∠BAC
4. Set the Equations Equal:
Since ∠DAB=∠EAC=60∘, we can substitute:
∠DAC=60∘+∠BAC
∠EAB=60∘+∠BAC
5. Conclude:
Since both expressions for ∠DAC and ∠EAB are equal:
∠DAC=∠EAB
Thus, we have proved that ∠DAC=∠EAB.
Part (ii): Proving DC=BE
1. Consider Triangles BAE and CAD:
We will show that triangles BAE and CAD are congruent.
2. Identify Corresponding Sides:
- AB=AD (sides of equilateral triangle ABD)
- AC=AE (sides of equilateral triangle ACE)
3. Use the Angle We Proved:
From part (i), we have:
- ∠EAB=∠DAC
4. Apply the Criteria for Congruence:
We have:
- Side AB=AD
- Side AC=AE
- Angle EAB=DAC
Therefore, by the Side-Angle-Side (SAS) congruence criterion:
△BAE≅△CAD
5. Conclude Using CPCTC:
From the congruence of triangles, we can conclude:
BE=DC(by Corresponding Parts of Congruent Triangles)
Final Conclusion:
- We have proved both parts:
1. ∠DAC=∠EAB
2. DC=BE
- Triangle ABC
- Equilateral triangle ABD on side AB
- Equilateral triangle ACE on side AC
1. ∠DAC=∠EAB
2. DC=BE
Since triangles ABD and ACE are equilateral, each angle in these triangles measures 60∘.
- Therefore, ∠ADB=60∘ and ∠AEC=60∘.
We know that:
- ∠DAB=∠EAC=60∘ (since they are angles of equilateral triangles).
Now, consider the angles ∠DAC and ∠EAB:
∠DAC=∠DAB+∠BAC
∠EAB=∠EAC+∠BAC
Since ∠DAB=∠EAC=60∘, we can substitute:
∠DAC=60∘+∠BAC
∠EAB=60∘+∠BAC
Since both expressions for ∠DAC and ∠EAB are equal:
∠DAC=∠EAB
Thus, we have proved that ∠DAC=∠EAB.
We will show that triangles BAE and CAD are congruent.
- AB=AD (sides of equilateral triangle ABD)
- AC=AE (sides of equilateral triangle ACE)
From part (i), we have:
- ∠EAB=∠DAC
We have:
- Side AB=AD
- Side AC=AE
- Angle EAB=DAC
△BAE≅△CAD
From the congruence of triangles, we can conclude:
BE=DC(by Corresponding Parts of Congruent Triangles)
- We have proved both parts:
1. ∠DAC=∠EAB
2. DC=BE
Topper's Solved these Questions
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Exercise 7b
Explore 15 Videos
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Revision Exercise (very Short Answer Questions)
Explore 10 Videos
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Problems From NCERT/exemplar
Explore 5 Videos
- SURFACE AREA AND VOLUMEBook:NAGEEN PRAKASHANChapter:SURFACE AREA AND VOLUMEExercise:Revision Exercise (long Answer Questions)
Explore 10 Videos
Similar Questions
Knowledge Check
Squares ABDE and ACFH are drawn externally on the sides AB and AC respectively of a scalene ΔABC. Which one of the following is correct?
ABH=CEBAD = AFCBF=CDDDF = EH
In ΔABC, BD and CE are perpendicluars to the sides AC and AB respectively and BD = CE. Prove that ΔBCD≅ΔCBE.
View SolutionThe square ABGH and ADEF are drawn on the sides AB and AD of a parallelogram ABCD. Prove (i) ∠FAH=∠ABC, (ii) FH = AC.
View SolutionP and Q are the points on sides AB and AC respectively of a ΔABC , such that PQ||BC .If AP∣PB=2:3 and AQ=4 cm , then the length of AC is ….. Cm .
View SolutionABC is an equilateral triangle, and AD and BE are perpendiculars to BC and AC respectively. Prove that: 1. AD=BE 2. BD=CE [ΔABD=ΔBCE.]
View SolutionABC is a triangle in which altitude BE and CF drawn on AC and AB respectively are equal. Prove that ΔBEC≅ΔCFB
View SolutionIn the given Fig. 3, in ΔABC,DandE are the mid point of the sides AB and AC respectively. Find the length of DE. Prove that DE=12BC.
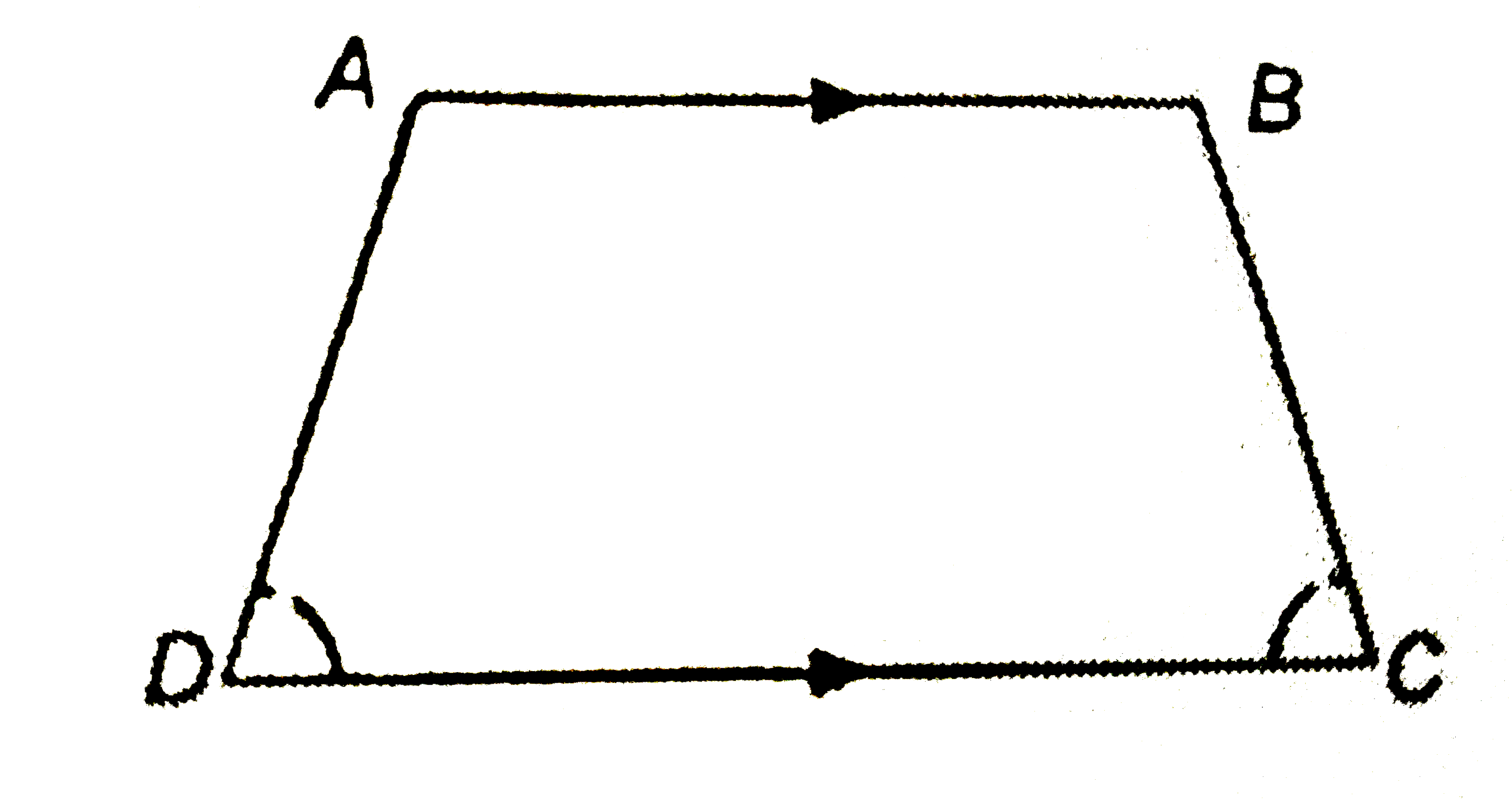
View SolutionIn the given figure, AB||DC and ∠D=∠C. Prove that :
(i) AD=BC
(ii) AC=BD
View Solution