ABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA Prove that (i) ΔABD≅ΔBAC (ii) BD = AC (iii) ∠ABD=∠BAC
∠DAB=∠CBA
AD=BC
∠ADC=∠BCD
AB||CD
In∠ABDand∠BAC
AB=AB
∠BAD=∠ABC
AD=BC
∠ABD≅∠BAC
BD=AC
∠ABD=∠BAC.
Similar Questions
In the given figure, ABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA.
Prove that (i) ΔABD≅ΔBAC,
(ii) BD = AC,
(iii) ∠ABD=∠BAC.

View SolutionABCD is quadrilateral in which AD=BCand∠DAB=∠CBA (see figure). Prove that
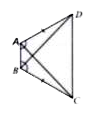
ΔABD≅ΔBAC
View SolutionABCD is quadrilateral in which AD=BCand∠DAB=∠CBA (see figure). Prove that

BD=AC
View SolutionIn quadrilateral ABCD, AD = BC and BD = CA. Prove that :
(i) ∠ADB=∠BCA
(ii) ∠DAB=∠CBA
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionIn quadrilateral ABCD, AB||CD and BC||AD. Show that
(i) ΔABD≅ΔCDB

View SolutionIn the given figure, quadrilateral ABCD is a quadrilateral in which AB = AD and BC = DC. Prove that (i) AC bisects ∠A and ∠B, (ii) AC.is the perpendicular bisector of BD.
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View SolutionIn a quadrilateral ABCD, AB = AD and CB = CD. Prove that :
(i) AC bisects angle BAD
(ii) AC is perpendicular bisector of BD.
View Solution
